Question

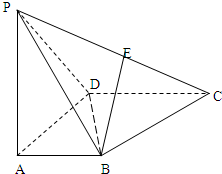如图所示，四棱锥P-ABCD的底面是直角梯形，PA⊥底面ABCD，AB⊥AD，CD⊥AD，CD=2AB，E为PC的中点，PA=AD=AB=1．
（1）证明：BE∥平面PAD；
（2）证明：BE⊥平面PDC；
（3）求三棱锥E-PBD的体积．

Answer 1

分析：（1）根据线面平行的判定定理即可证明：BE∥平面PAD；
（2）根据线面垂直的判定定理证明：BE⊥平面PDC；
（3）根据三棱锥的体积公式即可求三棱锥E-PBD的体积．

解答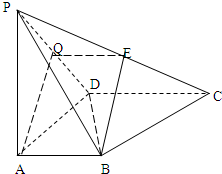：解：（1）证明：取PD中点Q，连结AQ、EQ．…（1分）
∵E为PC的中点，
∴EQ∥CD且EQ=

1

2

CD．…（2分）
又∵AB∥CD且AB=

1

2

CD，
∴EQ∥AB且EQ=AB．…（3分）
∴四边形ABED是平行四边形，
∴BE∥AQ．…（4分）
又∵BE?平面PAD，AQ?平面PAD，
∴BE∥平面PAD．…（5分）
（2）证明：∵PA⊥底面ABCD，∴PA⊥CD．…（6分）
又∵CD⊥AD，且PA∩AD=A，∴CD⊥平面PAD，∴CD⊥AQ．…（7分）
∵PA=AD，Q为PD的中点，∴AQ⊥PD，…（8分）
∵CD∩PD=D，∴AQ⊥平面PDC．…（9分）
∵BE∥AQ，∴BE⊥平面PDC．…（10分）
（3）解法一
∵E为PC的中点，
∴V_E-PBD=V_B-PDE=V_B-ECD=V_E-BCD．…（11分）
∵PA⊥底面ABCD，
∴点E到面BCD的距离d=

1

2

PA=

1

2

．…（12分）
∴S△BCD=

1

2

CD×AD=

1

2

×2×1=1．…（13分）
V_E-BCD=

1

3

S△BCD×d=

1

3

×1×

1

2

=

1

6

，
∵E为PC的中点，
∴VE-PBD=

1

6

．…（14分）
解法二
由前面证明可知：BE是三棱锥B-PDE的高，CD⊥PD．
在Rt△PAD中，PD=

PA2+AD2

=

2

，BE=AQ=

1

2

PD=

2

2

．…（11分）
S△PDE=

1

2

S△PDC=

1

2

×

1

2

×PD×DC=

2

2

，…（12分）
V_E-PBD=V_B-PDE…（13分）=

1

3

S△PDE×BE=

1

3

×

2

2

×

2

2

=

1

6

．…（14分）

点评：本题主要考查空间直线和平面平行或垂直的判断以及空间三棱锥的体积的计算，要求熟练掌握相应的判定定理．考查学生的推理能力．