题目内容
【题目】(本小题满分12分)已知函数![]() (
(![]() )的最小正周
)的最小正周
期为![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将函数![]() 的图像上各点的横坐标缩短到原来的
的图像上各点的横坐标缩短到原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]()
的图像,求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(1)1;(2)1.
【解析】试题分析:(Ⅰ)将函数式整理变形为![]() 的形式,由函数周期可求得
的形式,由函数周期可求得![]() 的值;(Ⅱ)由(Ⅰ)中求得的函数式按照平移规律得到函数
的值;(Ⅱ)由(Ⅰ)中求得的函数式按照平移规律得到函数![]() ,由定义域求得
,由定义域求得![]() 的取值范围,结合函数单调性可求得函数的最小值
的取值范围,结合函数单调性可求得函数的最小值
试题解析:(Ⅰ)∵f(x)=sin(π﹣ωx)cosωx+cos2ωx,
∴f(x)=sinωxcosωx+![]()
=![]() sin2ωx+
sin2ωx+![]() cos2ωx+
cos2ωx+![]()
=![]() sin(2ωx+
sin(2ωx+![]() )+
)+![]()
由于ω>0,依题意得![]() ,
,
所以ω=1;
(Ⅱ)由(Ⅰ)知f(x)=![]() sin(2x+
sin(2x+![]() )+
)+![]() ,
,
∴g(x)=f(2x)=![]() sin(4x+
sin(4x+![]() )+
)+![]()
∵0≤x≤![]() 时,
时,![]() ≤4x+
≤4x+![]() ≤
≤![]() ,
,
∴![]() ≤sin(4x+
≤sin(4x+![]() )≤1,
)≤1,
∴1≤g(x)≤![]() ,
,
g(x)在此区间内的最小值为1.

练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式:  ,
, ![]() =
=![]() .
.
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 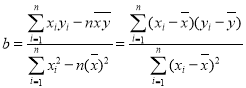 ,
, ![]() .
.