题目内容
已知{an}是正数组成的数列,a1=1,且点(| an |
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,bn+1=bn+2an,求数列{bn}的通项公式.
分析:(1)由已知得an+1-an=2,a1=1,所以数列{an}是以1 为首项,公差为2的等差数列,由此能求出an.
(2)由an=2n-1,知bn+1-bn=22n-1.bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1=22n-3+22n-5+…+23+21+1,由此能求出数列{bn}的通项公式.
(2)由an=2n-1,知bn+1-bn=22n-1.bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1=22n-3+22n-5+…+23+21+1,由此能求出数列{bn}的通项公式.
解答:解:(1)由已知得an+1=an+2,
即an+1-an=2…(3分)
又a1=1,所以数列{an}是以1 为首项,公差为2的等差数列
故an=1+(n-1)×2=2n-1…(4分)
(2)由(1)知an=2n-1,从而bn+1-bn=22n-1…(6分)
bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1…(8分)=22n-3+22n-5+…+23+21+1…(10分)
=
+1=
(4n+2)…(12分)
即an+1-an=2…(3分)
又a1=1,所以数列{an}是以1 为首项,公差为2的等差数列
故an=1+(n-1)×2=2n-1…(4分)
(2)由(1)知an=2n-1,从而bn+1-bn=22n-1…(6分)
bn=(bn-bn-1)+(bn-1-bn-2)+…+(b2-b1)+b1…(8分)=22n-3+22n-5+…+23+21+1…(10分)
=
| 2-22n-1 |
| 1-4 |
| 1 |
| 6 |
点评:本题考查数列的通项公式的求法,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
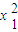 +
+ +…+
+…+ ,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B;
,B=x1x2+x2x3+…+xn-1xn+xnx1其中x1,x2,…xn都是正数,则A≤B; +
+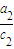 +
+ 的最小值为3;
的最小值为3; +
+ +…+
+…+ +
+ 的最小值为
的最小值为 .
.