题目内容
过点（-1，1）作直线与圆x2+y2=4相交，则所得弦的长度最短时，直线方程为分析：当所得弦的长度最短时，直线的斜率为
=1，用点斜式求得直线方程．
| -1 | ||
|
解答：解：圆x2+y2=4 的圆心A（0，0 ），所得弦的长度最短时，直线的斜率为
=1，
故直线的方程为 y-1=1（x+1），即x-y+2=0，
故答案为x-y+2=0．
| -1 | ||
|
故直线的方程为 y-1=1（x+1），即x-y+2=0，
故答案为x-y+2=0．
点评：本题考查用点斜式求直线方程的方法，求出弦的长度最短时直线的斜率为
=1，是解题的关键．
| -1 | ||
|
练习册系列答案
相关题目
如图，在直三棱柱ABC-A′B′C′中，点D是BC的中点，∠ACB=90°，AC=BC=1，AA′=2，
（广东卷理20）如图5所示，四棱锥
的底面
是半径为
的圆的内接四边形，其中
是圆的直径，
，
，
垂
，
分别是
上的点，且
，过点
作
的平行线交
于
．
所成角
的正弦值；
是直角三角形；
时，求
（广东卷理20）如图5所示，四棱锥
的底面
是半径为
的圆的内接四边形，其中
是圆的直径，
，
，
垂
，
分别是
上的点，且
，过点
作
的平行线交
于
．
所成角
的正弦值；
是直角三角形；
时，求
（
）上任意一点到两焦点距离之和为
，离心率为
，左、右焦点分别为
，
，点
是右准线上任意一点，过
的垂线
交椭圆于
点．
的标准方程；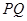
与直线
的斜率之积是定值；
与椭圆交于两个不同点
，在线段
上取点
，满足
，试证明点