题目内容
函数
的图象的对称点 ； 对称轴 ．
【答案】分析：利用正弦函数的图象的对称点即图象与x 轴的交点，过最高或最低点垂直于 x轴的直线是对称轴，求出对称点坐标和对称轴方程，转化计算可得答案．
解答：解：函数
的图象的对称点 即图象与x 轴的交点，∵2x+
=2kπ 时，k∈z，y=0，
即 x=kπ+
时，y=0，∴对称点为 （kπ+
，0），k∈z．
由 2x+
=kπ+
得 x=
π+
，k∈z，
故对称轴为 x=
π+
，k∈z．
故答案为 （kπ+
，0），k∈z；x=
π+
，k∈z．
点评：本题考查正弦函数的对称性，图象的对称点 即图象与x 轴的交点，过顶点垂直于 x轴的直线是对称轴．
解答：解：函数
的图象的对称点 即图象与x 轴的交点，∵2x+=2kπ 时，k∈z，y=0，即 x=kπ+
时，y=0，∴对称点为 （kπ+，0），k∈z．由 2x+
=kπ+ 得 x=π+，k∈z，故对称轴为 x=
π+，k∈z．故答案为 （kπ+
，0），k∈z；x=π+，k∈z．点评：本题考查正弦函数的对称性，图象的对称点 即图象与x 轴的交点，过顶点垂直于 x轴的直线是对称轴．
练习册系列答案
相关题目
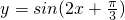的图象的对称点________； 对称轴________．