题目内容
已知:向量 ,设f(x)=(
,设f(x)=(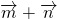 )
) -1.
-1.
(1)求f(x)的表达式;
(2)求函数f(x)的图象与其对称轴的交点的坐标.
解:(1)f(x)=(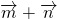 )
) -1=sin2x+
-1=sin2x+ sinxcosx+
sinxcosx+ …2
…2
= +
+ sin2+
sin2+ =sin(2x-
=sin(2x- )+1…5
)+1…5
(2)令2x- =2kπ+
=2kπ+ ,则x=kπ+
,则x=kπ+ ,k∈Z…7
,k∈Z…7
2x- =2kπ-
=2kπ- ,则x=kπ-
,则x=kπ- ,k∈Z…8
,k∈Z…8
∴函数f(x)的图象与其对称轴的交点的坐标为:(kπ+ ,2)或(kπ-
,2)或(kπ- ,0)k∈Z…10
,0)k∈Z…10
分析:(1)可利用向量的坐标运算与三角函数的倍角公式将f(x)=(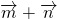 )
) -1化简为f(x)=sin(2x-
-1化简为f(x)=sin(2x- )+1;
)+1;
(2)求得f(x)=sin(2x- )+1的对称轴方程,即可得到函数f(x)的图象与其对称轴的交点的坐标.
)+1的对称轴方程,即可得到函数f(x)的图象与其对称轴的交点的坐标.
点评:本题考查三角函数中的恒等变换应用,易错点在于所求交点的坐标为:(kπ+ ,2)或(kπ-
,2)或(kπ- ,0),k∈Z.属于中档题.
,0),k∈Z.属于中档题.
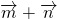 )
) -1=sin2x+
-1=sin2x+ sinxcosx+
sinxcosx+ …2
…2=
 +
+ sin2+
sin2+ =sin(2x-
=sin(2x- )+1…5
)+1…5(2)令2x-
 =2kπ+
=2kπ+ ,则x=kπ+
,则x=kπ+ ,k∈Z…7
,k∈Z…72x-
 =2kπ-
=2kπ- ,则x=kπ-
,则x=kπ- ,k∈Z…8
,k∈Z…8∴函数f(x)的图象与其对称轴的交点的坐标为:(kπ+
 ,2)或(kπ-
,2)或(kπ- ,0)k∈Z…10
,0)k∈Z…10分析:(1)可利用向量的坐标运算与三角函数的倍角公式将f(x)=(
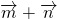 )
) -1化简为f(x)=sin(2x-
-1化简为f(x)=sin(2x- )+1;
)+1;(2)求得f(x)=sin(2x-
 )+1的对称轴方程,即可得到函数f(x)的图象与其对称轴的交点的坐标.
)+1的对称轴方程,即可得到函数f(x)的图象与其对称轴的交点的坐标.点评:本题考查三角函数中的恒等变换应用,易错点在于所求交点的坐标为:(kπ+
 ,2)或(kπ-
,2)或(kπ- ,0),k∈Z.属于中档题.
,0),k∈Z.属于中档题. 
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
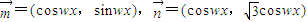 ,设函数
,设函数 且f(x)的最小正周期为2π.
且f(x)的最小正周期为2π. ,求证:f(x)>g(x).
,求证:f(x)>g(x). ,设函数
,设函数 且f(x)的最小正周期为2π.
且f(x)的最小正周期为2π. ,求证:f(x)>g(x).
,求证:f(x)>g(x). ,设f(x)=(
,设f(x)=( )
) -1.
-1. ,设f(x)=(
,设f(x)=( )
) -1.
-1.