题目内容
在△ABC中,角A,B,C所对边分别是a,b,c,且3bsinC-5csinBcosA=0(1)求sinA;(2)若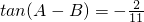 ,求tanC.
,求tanC.
解:(1)由正弦定理 =
= 得:bsinC=csinB.
得:bsinC=csinB.
又3bsinC-5csinBcosA=0,
∴bsinC(3-5cosA)=0,
∵bsinC≠0,∴3-5cosA=0,即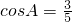 .
.
又A∈(0,π),
∴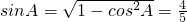 ;…(4分)
;…(4分)
(2)由(1)知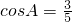 ,
,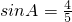 ,
,
∴ .
.
因为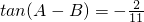 ,
,
所以 ,
,
所以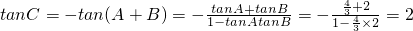 .…(8分)
.…(8分)
分析:(1)根据正弦定理得到bsinC=csinB,代入已知的等式中,提取bsinC,根据bsinC不为0,可得cosA的值,由A为三角形的内角,利用同角三角函数间的平方关系即可求出sinA的值;
(2)由(1)求出的sinA和cosA的值,利用同角三角函数间的基本关系求出tanA的值,根据B=A-(A-B),利用两角和与差的正切函数公式表示出tanB=tan[A-(A-B)],把tanA和tan(A-B)的值代入求出tanB的值,再根据诱导公式及三角形的内角和定理得到tanC=-tan(A+B),利用两角和与差的正切函数公式化简后,将tanA和tanB的值代入即可求出tanC的值.
点评:此题考查了正弦定理,同角三角函数间的基本关系,两角和与差的正切函数公式,熟练掌握定理及公式是解本题的关键,同时注意角度的灵活变换.
 =
= 得:bsinC=csinB.
得:bsinC=csinB.又3bsinC-5csinBcosA=0,
∴bsinC(3-5cosA)=0,
∵bsinC≠0,∴3-5cosA=0,即
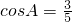 .
.又A∈(0,π),
∴
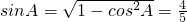 ;…(4分)
;…(4分)(2)由(1)知
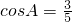 ,
,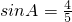 ,
,∴
 .
.因为
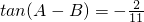 ,
,所以
 ,
,所以
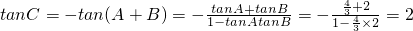 .…(8分)
.…(8分)分析:(1)根据正弦定理得到bsinC=csinB,代入已知的等式中,提取bsinC,根据bsinC不为0,可得cosA的值,由A为三角形的内角,利用同角三角函数间的平方关系即可求出sinA的值;
(2)由(1)求出的sinA和cosA的值,利用同角三角函数间的基本关系求出tanA的值,根据B=A-(A-B),利用两角和与差的正切函数公式表示出tanB=tan[A-(A-B)],把tanA和tan(A-B)的值代入求出tanB的值,再根据诱导公式及三角形的内角和定理得到tanC=-tan(A+B),利用两角和与差的正切函数公式化简后,将tanA和tanB的值代入即可求出tanC的值.
点评:此题考查了正弦定理,同角三角函数间的基本关系,两角和与差的正切函数公式,熟练掌握定理及公式是解本题的关键,同时注意角度的灵活变换.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |