题目内容
14.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点分别为A和B,且$\overrightarrow{AB}$与$\overrightarrow{n}$=(1,-$\frac{\sqrt{3}}{2}$)共线,若点O,F分别为椭圆C的中心和左焦点,点P为椭圆C上任意一点,且$\overrightarrow{OP}$•$\overrightarrow{FP}$的最大值为6,则椭圆C的长轴长为4.分析 通过$\overrightarrow{AB}$与$\overrightarrow{n}$=(1,-$\frac{\sqrt{3}}{2}$)共线可知b=$\frac{\sqrt{3}}{2}$a,从而可知F(-$\frac{a}{2}$,0),通过设P(x,y),进而化简可知$\overrightarrow{OP}$•$\overrightarrow{FP}$=$\frac{1}{4}$(x+a)2+$\frac{{a}^{2}}{2}$,利用-a≤x≤a可知$\frac{1}{4}$(a+a)2+$\frac{{a}^{2}}{2}$=6,计算即得结论.
解答 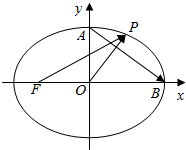 解:依题意,A(0,b),B(a,0),O(0,0),
解:依题意,A(0,b),B(a,0),O(0,0),
∴$\overrightarrow{AB}$=(a,-b),
又∵$\overrightarrow{AB}$与$\overrightarrow{n}$=(1,-$\frac{\sqrt{3}}{2}$)共线,
∴-$\frac{\sqrt{3}}{2}$a=-b,即b=$\frac{\sqrt{3}}{2}$a,
∴椭圆方程可化为:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{4{y}^{2}}{3{a}^{2}}$=1,
∴F(-$\frac{a}{2}$,0),
设P(x,y),则$\overrightarrow{OP}$•$\overrightarrow{FP}$=(x,y)•(x+$\frac{a}{2}$,y)
=$\frac{a}{2}$x+x2+y2
=$\frac{a}{2}$x+x2+$\frac{3}{4}$(a2-x2)
=$\frac{1}{4}$x2+$\frac{a}{2}$x+$\frac{3}{4}$a2
=$\frac{1}{4}$(x+a)2+$\frac{{a}^{2}}{2}$,
∵-a≤x≤a,
∴当x=a时,$\overrightarrow{OP}$•$\overrightarrow{FP}$取最大值为6,
∴$\frac{1}{4}$(a+a)2+$\frac{{a}^{2}}{2}$=6,
解得:a=2或a=-2(舍),
∴长轴长2a=4,
故答案为:4.
点评 本题考查椭圆的简单性质,考查运算求解能力,注意解题方法的积累,属于中档题.注:本题亦可通过两向量同向时数量积最大从而直接确定点P为右端点.

| A. | 曲线C关于坐标原点对称 | B. | 曲线C关于y轴对称 | ||
| C. | 曲线C关于x轴对称 | D. | 曲线C过坐标原点 |
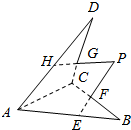 已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点,且直线EF交直线HG于点P,则点P的位置是必处在( )的上面.
已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点,且直线EF交直线HG于点P,则点P的位置是必处在( )的上面.| A. | BD | B. | AD | C. | AC | D. | 平面BCD之内 |
| A. | (0,2) | B. | (0,3i ) | C. | (0,3) | D. | (0,2i) |
| A. | (1,2) | B. | (2,+∞) | C. | (1,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,+∞) |
| A. | (1,$\sqrt{2}$] | B. | (1,$\sqrt{2}$) | C. | ($\sqrt{2}$,+∞) | D. | [$\sqrt{2}$,+∞) |