题目内容
在等差数列{an}中,(1)已知a2+a3+a23+a24=48,求a13;
(2)已知a2+a3+a4+a5=34,a2·a5=52,求公差d.
解:(1)根据已知条件a2+a3+a23+a24=48,得4a13=48,∴a13=12.
(2)由a2+a3+a4+a5=34,得2(a2+a5)=34,即a2+a5=17.
解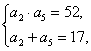 得
得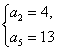 或
或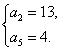
∴d=![]() =
=![]() =3或d=
=3或d=![]() =
=![]() =-3.
=-3.
点评:等差数列{an}中最基本的量是首项a1和公差d,利用性质解决等差数列问题较为简单方便,当然利用已知条件列出关于a1、d的方程问题也是可以解决的.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目