Question

已知f(x)＝m(x－2m)(x＋m＋3)，g(x)＝2^x－2.若同时满足条件：

①∀x∈R，f(x)<0或g(x)<0；

②∃x∈(－∞，－4)，f(x)g(x)<0，

则m的取值范围是________．

Answer 1

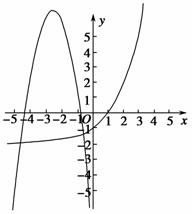
解析　当x<1时，g(x)<0，当x>1时，g(x)>0，当x＝1时，g(x)＝0，m＝0不符合要求；当m>0时，根据函数f(x)和函数g(x)的单调性，一定存在区间[a，＋∞)使f(x)≥0且g(x)≥0，故m>0时不符合第①条的要求；当m<0时，如图所示，如果符合①的要求，则函数f(x)的两个零点都得小于1，如果符合第②条要求，则函数f(x)至少有一个零点小于－4，问题等价于函数f(x)有两个不相等的零点，其中较大的零点小于1，较小的零点小于－4，函数f(x)的两个零点是2m，－(m＋3)，故m满足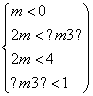或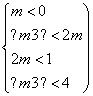解第一个不等式组得－4<m<－2，第二个不等式组无解，故所求m的取值范围是(－4，－2)．

答案　(－4，－2)