题目内容
已知函数f(x)=a(x-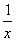 )-lnx,
)-lnx,
(Ⅰ)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若函数f(x)在其定义域内为增函数,求a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,设函数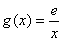 ,若在[1,e]上至少存在一点x0,使得f(x0)≥g(x0)成立,求实数a的取值范围。
,若在[1,e]上至少存在一点x0,使得f(x0)≥g(x0)成立,求实数a的取值范围。
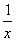 )-lnx,
)-lnx,(Ⅰ)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)若函数f(x)在其定义域内为增函数,求a的取值范围;
(Ⅲ)在(Ⅱ)的条件下,设函数
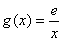 ,若在[1,e]上至少存在一点x0,使得f(x0)≥g(x0)成立,求实数a的取值范围。
,若在[1,e]上至少存在一点x0,使得f(x0)≥g(x0)成立,求实数a的取值范围。解:(Ⅰ)当a=1时,函数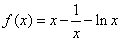 ,
,
f(1)=1-1-ln1=0,
f′(x)=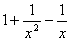 ,
,
曲线f(x)在点(1,f(1))处的切线的斜率为f′(1)=1+1-1=1,
从而曲线f(x)在点(1,f(1))处的切线方程为y-0=x-1,即y=x-1;
(Ⅱ)f′(x)=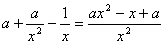 ,
,
要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0在(0,+∞)内恒成立,
即ax2-x+a≥0,得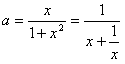 恒成立,
恒成立,
由于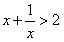 ,
,
∴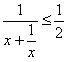 ,∴
,∴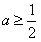 ,
,
∴f(x)在(0,+∞)内为增函数,实数a的取值范围是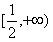 ;
;
(Ⅲ)∵在[1,e]上是减函数,
∴x=e时,g(x)min=1;x=1时,g(x)max=e,即 g(x)∈[1,e],
f′(x)=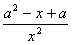 ,令h(x)=ax2-x+a,
,令h(x)=ax2-x+a,
当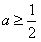 时,由(Ⅱ)知f(x)在[1,e]上是增函数,f(1)=0<1,
时,由(Ⅱ)知f(x)在[1,e]上是增函数,f(1)=0<1,
又g(x)在[1,e]上是减函数,
故只需f(x)max≥g(x)min,x∈[1,e],
而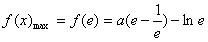 ,g(x)min=1,
,g(x)min=1,
即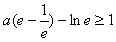 ,解得
,解得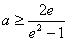 ,
,
所以实数a的取值范围是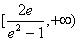 。
。
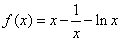 ,
,f(1)=1-1-ln1=0,
f′(x)=
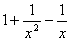 ,
,曲线f(x)在点(1,f(1))处的切线的斜率为f′(1)=1+1-1=1,
从而曲线f(x)在点(1,f(1))处的切线方程为y-0=x-1,即y=x-1;
(Ⅱ)f′(x)=
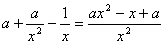 ,
,要使f(x)在定义域(0,+∞)内是增函数,只需f′(x)≥0在(0,+∞)内恒成立,
即ax2-x+a≥0,得
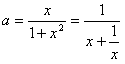 恒成立,
恒成立,由于
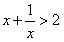 ,
,∴
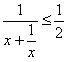 ,∴
,∴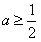 ,
,∴f(x)在(0,+∞)内为增函数,实数a的取值范围是
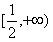 ;
;(Ⅲ)∵在[1,e]上是减函数,
∴x=e时,g(x)min=1;x=1时,g(x)max=e,即 g(x)∈[1,e],
f′(x)=
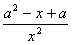 ,令h(x)=ax2-x+a,
,令h(x)=ax2-x+a,当
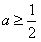 时,由(Ⅱ)知f(x)在[1,e]上是增函数,f(1)=0<1,
时,由(Ⅱ)知f(x)在[1,e]上是增函数,f(1)=0<1,又g(x)在[1,e]上是减函数,
故只需f(x)max≥g(x)min,x∈[1,e],
而
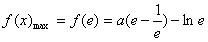 ,g(x)min=1,
,g(x)min=1,即
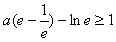 ,解得
,解得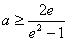 ,
,所以实数a的取值范围是
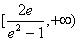 。
。
练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目