题目内容
设无穷等差数列{an}的前n项和为Sn.
(Ⅰ)若首项a1=
,公差d=1.求满足Sk2=(Sk)2的正整数k;
(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有Sk2=(Sk)2成立.
(Ⅰ)若首项a1=
| 3 |
| 2 |
(Ⅱ)求所有的无穷等差数列{an},使得对于一切正整数k都有Sk2=(Sk)2成立.
(Ⅰ)∵首项a1=
,公差d=1.
∴Sn=na1+
d=
n+
=
n2+n,
由Sk2=(Sk)2得
(k2)2+k2=(
k2+k )2,
即
k4- k3=0,
∵k是正整数,∴k=4.…(5分)
(Ⅱ)设数列
的公差为d,
则在Sk2=(Sk)2中分别取k=1,和k=2得
,
即
由①得a1=0或a1=1,
当a1=0时,代入②得d=0或d=6.若a1=0,d=0则本题成立;
若a1=0,d=6,则an=6(n-1),
由S3=18,(S3)2=324,S9=216知S9≠(S3)2,故所得数列不符合题意;
当a1=1时,代入②得4+6d=(2+d)2,
解得d=0或d=2.
若a=1,d=0则an=1,Sn=n从而Sk2=(Sk)2成立;
若a1=1,d=2,则an=2n-1,Sn=n2,
从而Sk2=(Sk)2成立.
综上所述,只有3个满足条件的无穷等差数列:
①an=0; ②an=1;③an=2n-1.
| 3 |
| 2 |
∴Sn=na1+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| n(n-1) |
| 2 |
| 1 |
| 2 |
由Sk2=(Sk)2得
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 4 |
∵k是正整数,∴k=4.…(5分)
(Ⅱ)设数列
| a |
| 2 |
则在Sk2=(Sk)2中分别取k=1,和k=2得
|
即
|
由①得a1=0或a1=1,
当a1=0时,代入②得d=0或d=6.若a1=0,d=0则本题成立;
若a1=0,d=6,则an=6(n-1),
由S3=18,(S3)2=324,S9=216知S9≠(S3)2,故所得数列不符合题意;
当a1=1时,代入②得4+6d=(2+d)2,
解得d=0或d=2.
若a=1,d=0则an=1,Sn=n从而Sk2=(Sk)2成立;
若a1=1,d=2,则an=2n-1,Sn=n2,
从而Sk2=(Sk)2成立.
综上所述,只有3个满足条件的无穷等差数列:
①an=0; ②an=1;③an=2n-1.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 ,公差d=1.求满足
,公差d=1.求满足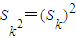 的正整数k;
的正整数k;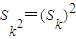 成立.
成立.