题目内容
设两点A(3,1),B(-1,5),直线l通过线段AB的中点C.(1)若l⊥AB,求直线l的倾斜角的大小;
(2)若l的倾斜角θ满足
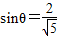 ,求l的方程.
,求l的方程.
【答案】分析:(1)由中点坐标公式可得中点C的坐标,进而由垂直关系得斜率,最后点斜式可得方程,化为一般式即可.
(2)由 ,可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.
,可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.
解答:解:(1)由中点坐标公式可得中点C的坐标为(1,3)
由l⊥AB得,直线l的斜率k=- =1,
=1,
故方程为y-3=x-1,化为一般式可得:x-y+2=0.
(2)由 ,可得tanθ=2或-2,
,可得tanθ=2或-2,
又直线过点C(1,3),故方程为y-3=2(x-1),或y-3=-2(x-1)
化为一般式可得:2x-y+1=0或2x+y-5=0.
点评:本题考查直线方程的求解,涉及分类的思想,属基础题.
(2)由
 ,可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.
,可得tanα=1或-1,进而由点斜式可得方程,化为一般式即可.解答:解:(1)由中点坐标公式可得中点C的坐标为(1,3)
由l⊥AB得,直线l的斜率k=-
 =1,
=1,故方程为y-3=x-1,化为一般式可得:x-y+2=0.
(2)由
 ,可得tanθ=2或-2,
,可得tanθ=2或-2,又直线过点C(1,3),故方程为y-3=2(x-1),或y-3=-2(x-1)
化为一般式可得:2x-y+1=0或2x+y-5=0.
点评:本题考查直线方程的求解,涉及分类的思想,属基础题.

练习册系列答案
相关题目