题目内容
在下列函数中:①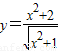 ;②
;②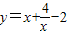 ;③
;③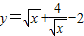 ;④y=|x+
;④y=|x+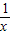 |;⑤
|;⑤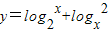 其中x>0且x≠1;⑥y=3x+3-x.其中最小值为2的函数是 (填入序号).
其中x>0且x≠1;⑥y=3x+3-x.其中最小值为2的函数是 (填入序号).
【答案】分析:①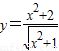 =
=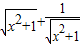 ≥2,可判断
≥2,可判断
②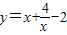 ,当x<0时,
,当x<0时,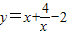 =
=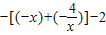
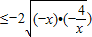 -2可判断
-2可判断
③由基本不等式可得,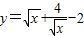
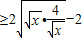 =2,可判断
=2,可判断
④y=|x+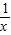 |=
|=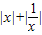 ≥2可判断
≥2可判断
⑤当log2x<0时,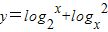 ≤-2可判断
≤-2可判断
⑥y=3x+3-x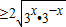 =2当且仅当3x=3-x即x=0时取等号可判断
=2当且仅当3x=3-x即x=0时取等号可判断
解答:解:①∵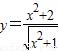 =
=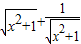 ≥2,当且仅当x=0时取等号,故①正确
≥2,当且仅当x=0时取等号,故①正确
②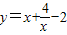 ,当x<0时,
,当x<0时,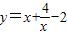 =
=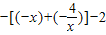
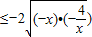 -2=-6,故②错误
-2=-6,故②错误
③由基本不等式可得,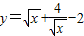
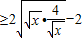 =2,③正确
=2,③正确
④y=|x+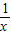 |=
|=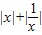 ≥2;④正确
≥2;④正确
⑤当log2x<0时,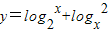 ≤-2;⑤错误
≤-2;⑤错误
⑥y=3x+3-x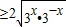 =2当且仅当3x=3-x即x=0时取等号,⑥正确
=2当且仅当3x=3-x即x=0时取等号,⑥正确
故答案为:①③④⑥
点评:本题主要考查了基本不等式在求解函数的最值中的应用,解题的关键是基本不等式的应用条件的判断
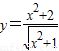 =
=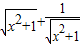 ≥2,可判断
≥2,可判断②
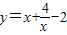 ,当x<0时,
,当x<0时,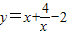 =
=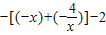
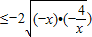 -2可判断
-2可判断③由基本不等式可得,
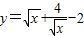
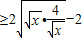 =2,可判断
=2,可判断④y=|x+
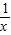 |=
|=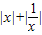 ≥2可判断
≥2可判断⑤当log2x<0时,
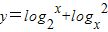 ≤-2可判断
≤-2可判断⑥y=3x+3-x
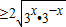 =2当且仅当3x=3-x即x=0时取等号可判断
=2当且仅当3x=3-x即x=0时取等号可判断解答:解:①∵
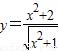 =
=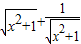 ≥2,当且仅当x=0时取等号,故①正确
≥2,当且仅当x=0时取等号,故①正确②
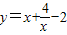 ,当x<0时,
,当x<0时,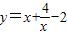 =
=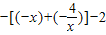
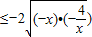 -2=-6,故②错误
-2=-6,故②错误③由基本不等式可得,
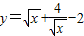
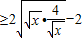 =2,③正确
=2,③正确④y=|x+
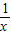 |=
|=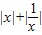 ≥2;④正确
≥2;④正确⑤当log2x<0时,
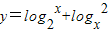 ≤-2;⑤错误
≤-2;⑤错误⑥y=3x+3-x
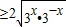 =2当且仅当3x=3-x即x=0时取等号,⑥正确
=2当且仅当3x=3-x即x=0时取等号,⑥正确故答案为:①③④⑥
点评:本题主要考查了基本不等式在求解函数的最值中的应用,解题的关键是基本不等式的应用条件的判断

练习册系列答案
相关题目
在下列函数中,最小值不是2的是( )
A、y=|x|+
| ||||
B、y=
| ||||
| C、y=lgx+logx10 | ||||
| D、y=3x+3-x |
 若对?x1、x2∈D,都有f(
若对?x1、x2∈D,都有f(