题目内容
(2013•宿迁一模)已知双曲线
-
=1(a>0,b>0),A,C分别是双曲线虚轴的上、下端点,B,F分别是双曲线的左顶点和左焦点.若双曲线的离心率为2,则
与
夹角的余弦值为
.
| x2 |
| a2 |
| y2 |
| b2 |
| BA |
| CF |
| ||
| 14 |
| ||
| 14 |
分析:利用双曲线的简单性质求出A、C、B、F各个点的坐标,再利用两个向量的夹角公式以及
=2,求出cosθ=
的值.
| c |
| a |
| ||||
|
|
解答:解:由题意可得由题意得A(0,b),C(0,-b),B(-a,0),F(-c,0),
=2.
∴
=(a,b),
=(-c,b). 设
与
的夹角为θ,则cosθ=
=
=
=
=
,
故答案为
.
| c |
| a |
∴
| BA |
| CF |
| BA |
| CF |
| ||||
|
|
| b2-ac | ||||
|
| c2-a2-ac | ||
c
|
| a2 | ||
2a
|
| ||
| 14 |
故答案为
| ||
| 14 |
点评:本题主要考查双曲线的简单性质的应用,两个向量的夹角公式,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
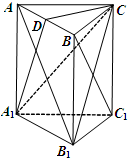 (2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.
(2013•宿迁一模)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,BC=BB1,D为AB的中点.