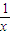题目内容
下列各命题中，正确的命题为（ ）
分析：利用平面向量的相关概念和应用进行判断．
解答：解：A．两个有共同起点且共线的向量，由于向量长度不一定相同，所以终点不一定相同，所以A错误．
B．模为0的向量为零向量，零向量和任一向量平行，所以B正确．
C．有向线段可以直观的表示向量，但不是向量，所以C错误．
D．向量的长度相等，但方向不一定相同，所以D错误．
故选B．
B．模为0的向量为零向量，零向量和任一向量平行，所以B正确．
C．有向线段可以直观的表示向量，但不是向量，所以C错误．
D．向量的长度相等，但方向不一定相同，所以D错误．
故选B．
点评：本题主要考查与向量有关的命题的真假判断，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
已知y=f（x）=ln|x|，则下列各命题中，正确的命题是（ ）
A、x＞0时，f'（x）=
| ||||
B、x＞0时，f'（x）=
| ||||
C、x≠0时，都有f'（x）=
| ||||
| D、∵x=0时f（x）无意义，∴对y=ln|x|不能求导 |
|=|
|⇒
=
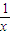，x＜0时，f'（x）=-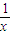
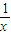，x＜0时，f'（x）无意义