题目内容
 如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上点,且满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点为O.
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,3AD=DC=3,AB=2,E是DC上点,且满足DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=60°,设AC与BE的交点为O.(1)试用基向量
| AB |
| AE |
| AD1 |
| OD1 |
(2)求异面直线OD1与AE所成角的余弦值;
(3)判断平面D1AE与平面ABCE是否垂直?并说明理由.
分析:(1)根据向量的减法可知
=
-
,而O为BE的中点可知
=
(
+
),即可用基向量
,
,
表示向量
;
(2)设异面直线OD1与AE所成的角为θ,然后根据向量的夹角公式cosθ=|cos<
,
>|=|
|进行求解;
(3)取AE的中点M,欲证平面D1AE⊥平面ABCE,根据面面垂直的判定定理可知在平面D1AE内一直线与平面ABCE垂直,而根据向量的垂直关系可知D1M⊥AE,D1M⊥AB,AE∩AB=A,满足线面垂直的判定定理,则D1M⊥平面ABCE,即可证得平面D1AE⊥平面ABCE.
| OD1 |
| AD1 |
| AO |
| AO |
| 1 |
| 2 |
| AB |
| AE |
| AB |
| AE |
| AD1 |
| OD1 |
(2)设异面直线OD1与AE所成的角为θ,然后根据向量的夹角公式cosθ=|cos<
| OD1 |
| AE |
| ||||
|
|
(3)取AE的中点M,欲证平面D1AE⊥平面ABCE,根据面面垂直的判定定理可知在平面D1AE内一直线与平面ABCE垂直,而根据向量的垂直关系可知D1M⊥AE,D1M⊥AB,AE∩AB=A,满足线面垂直的判定定理,则D1M⊥平面ABCE,即可证得平面D1AE⊥平面ABCE.
解答: 解:(1)∵AB∥CE,AB=CE=2,
解:(1)∵AB∥CE,AB=CE=2,
∴四边形ABCE是平行四边形,∴O为BE的中点.
∴
=
-
=
-
(
+
)
=
-
-
.
(2)设异面直线OD1与AE所成的角为θ,
则cosθ=|cos<
,
>|=|
|,
∵
•
=(
-
-
)•
=
•
-
•
-
|
|2
=1×
×cos45°-
×2×
×cos45°-
×(
)2
=-1,
|
|=
=
,
∴cosθ=|
|=|
|=
.
故异面直线OD1与AE所成角的余弦值为
.
(3)平面D1AE⊥平面ABCE.证明如下:
取AE的中点M,则
=
-
=
-
,
∴
•
=(
-
)•
=
|
|2-
•
=
×(
)2-1×
×cos45°=0.
∴
⊥
.∴D1M⊥AE.
∵
•
=(
-
)•
=
•
-
•
=
×
×2×cos45°-1×2×cos60°=0,
∴
⊥
,∴D1M⊥AB.
又AE∩AB=A,AE、AB?平面ABCE,
∴D1M⊥平面ABCE.
∵D1M?平面D1AE,
∴平面D1AE⊥平面ABCE.
 解:(1)∵AB∥CE,AB=CE=2,
解:(1)∵AB∥CE,AB=CE=2,∴四边形ABCE是平行四边形,∴O为BE的中点.
∴
| OD1 |
| AD1 |
| AO |
| AD1 |
| 1 |
| 2 |
| AB |
| AE |
=
| AD1 |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AE |
(2)设异面直线OD1与AE所成的角为θ,
则cosθ=|cos<
| OD1 |
| AE |
| ||||
|
|
∵
| OD1 |
| AE |
| AD1 |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
| AE |
| AE |
=
| AD1 |
| AE |
| 1 |
| 2 |
| AB |
| AE |
| 1 |
| 2 |
| AE |
=1×
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
=-1,
|
| OD1 |
(
|
| ||
| 2 |
∴cosθ=|
| ||||
|
|
| -1 | ||||||
|
| ||
| 3 |
故异面直线OD1与AE所成角的余弦值为
| ||
| 3 |
(3)平面D1AE⊥平面ABCE.证明如下:
取AE的中点M,则
| D1M |
| AM |
| AD1 |
| 1 |
| 2 |
| AE |
| AD1 |
∴
| D1M |
| AE |
| 1 |
| 2 |
| AE |
| AD1 |
| AE |
=
| 1 |
| 2 |
| AE |
| AD1 |
| AE |
=
| 1 |
| 2 |
| 2 |
| 2 |
∴
| D1M |
| AE |
∵
| D1M |
| AB |
| 1 |
| 2 |
| AE |
| AD1 |
| AB |
=
| 1 |
| 2 |
| AE |
| AB |
| AD1 |
| AB |
=
| 1 |
| 2 |
| 2 |
∴
| D1M |
| AB |
又AE∩AB=A,AE、AB?平面ABCE,
∴D1M⊥平面ABCE.
∵D1M?平面D1AE,
∴平面D1AE⊥平面ABCE.
点评:本小题主要考查平面与平面垂直的判定,以及异面直线及其所成的角和空间向量等有关知识,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
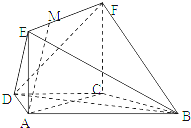 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.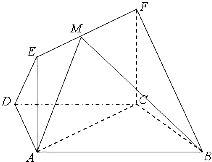 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.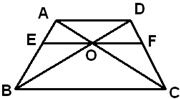 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.