Question

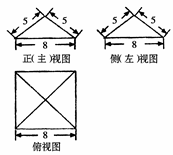
如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，
俯视图是半径为1的半圆，则该几何体的体积是（    ）

A．

B．

C．

D．

Answer 1

A

解析考点：由三视图求面积、体积．
专题：计算题．
分析：由三视图知几何体的直观图是半个圆锥，再根据其中正视图是腰长为2的等腰三角形，我们易得圆锥的底面直径为2，母线为为2，故圆锥的底面半径为1，高为，代入圆锥体积公式即可得到答案．
解答：解：由三视图知几何体的直观图是半个圆锥，
又∵正视图是腰长为2的等腰三角形
∴r=1，h=
∴v==π
故选：A．
点评：本题考查的知识点是由三视图求体积，其中根据三视图判断出几何的形状及相关几何量（底面半径，高等）的大小是解答的关键．