题目内容
设函数f(x)=2x,对于任意的x1,x2(x1≠x2),有下列命题
①f(x1+x2)=f(x1)•f(x2);②f(x1•x2)=f(x1)+f(x2);③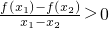 ;④
;④ .其中正确的命题序号是 ________.
.其中正确的命题序号是 ________.
①③④
分析:根据指数的运算性质和指数函数的单调性以及凹凸性对①②③④进行逐一进行判定即可.
解答:
 =
=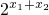 ,所以对于①成立,
,所以对于①成立,
 +
+ ≠
≠ ,所以对于②不成立,
,所以对于②不成立,
函数f(x)=2x,在R上是单调递增函数,
若x1>x2则f(x1)>f(x2),则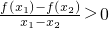 ,
,
若x1<x2则f(x1)<f(x2),则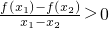 ,故③正确
,故③正确
 说明函数是凹函数,而函数f(x)=2x是凹函数,故④正确
说明函数是凹函数,而函数f(x)=2x是凹函数,故④正确
故答案为:①③④
点评:本题考查指数函数的性质,指数函数、对数函数是高考考查的重点内容之一,本节主要帮助考生掌握两种函数的概念、图象和性质.
分析:根据指数的运算性质和指数函数的单调性以及凹凸性对①②③④进行逐一进行判定即可.
解答:

 =
=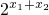 ,所以对于①成立,
,所以对于①成立, +
+ ≠
≠ ,所以对于②不成立,
,所以对于②不成立,函数f(x)=2x,在R上是单调递增函数,
若x1>x2则f(x1)>f(x2),则
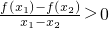 ,
,若x1<x2则f(x1)<f(x2),则
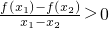 ,故③正确
,故③正确 说明函数是凹函数,而函数f(x)=2x是凹函数,故④正确
说明函数是凹函数,而函数f(x)=2x是凹函数,故④正确故答案为:①③④
点评:本题考查指数函数的性质,指数函数、对数函数是高考考查的重点内容之一,本节主要帮助考生掌握两种函数的概念、图象和性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目