题目内容
已知椭圆E: 的左、右焦点分别为F1、F2,上、下顶点分别为B1、B2,四边形B1F1B2F2的一个内角等于
的左、右焦点分别为F1、F2,上、下顶点分别为B1、B2,四边形B1F1B2F2的一个内角等于 ,椭圆过点P(1,
,椭圆过点P(1, ).
).
(1)求椭圆E的方程;
(2)直线l的斜率等于椭圆E的离心率,且交椭圆于A、B两点,直线PA和PB分别交x轴于点M、N,求证:|PM|=|PN|.
解:(1)由b> ,
,
知 ,
,
∴ ,
,
设所求椭圆方程为 ,
,
把点P(1, )代入,得b2=3,a2=4,
)代入,得b2=3,a2=4,
∴椭圆方程为 .
.
(2)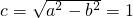 ,离心率
,离心率 ,
,
设直线l的方程为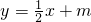 ,
,
代入椭圆方程,整理得x2+mx+m2-3=0,
∴x1+x2=-m,x1x2=m2-3,
要证|PM|=|PN|,只需证直线PA的斜率k1与直线PB的斜率k2互为相反数,
k1+k2=
∵(2y1-3)(x2-1)+(2y2-3)(x1-1)
=(x1+2m-3)(x2-1)+(x2+2m-3)(x1-1)
=2x1x2+(2m-4)(x1+x2)+6-4m
=2(m2-3)+(2m-4)(-m)+6-4m=0
所以,k1+k2=0,
因此|PM|=|PN|.
分析:(1)由b> ,知
,知 ,所以
,所以 ,设所求椭圆方程为
,设所求椭圆方程为 ,把点P(1,
,把点P(1, )代入,能求出椭圆方程.
)代入,能求出椭圆方程.
(2)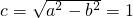 ,离心率
,离心率 ,设直线l的方程为
,设直线l的方程为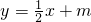 ,代入椭圆方程,得x2+mx+m2-3=0,所以x1+x2=-m,x1x2=m2-3,要证|PM|=|PN|,只需证直线PA的斜率k1与直线PB的斜率k2互为相反数.
,代入椭圆方程,得x2+mx+m2-3=0,所以x1+x2=-m,x1x2=m2-3,要证|PM|=|PN|,只需证直线PA的斜率k1与直线PB的斜率k2互为相反数.
点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.
 ,
,知
 ,
,∴
 ,
,设所求椭圆方程为
 ,
,把点P(1,
 )代入,得b2=3,a2=4,
)代入,得b2=3,a2=4,∴椭圆方程为
 .
.(2)
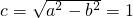 ,离心率
,离心率 ,
,设直线l的方程为
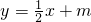 ,
,代入椭圆方程,整理得x2+mx+m2-3=0,
∴x1+x2=-m,x1x2=m2-3,
要证|PM|=|PN|,只需证直线PA的斜率k1与直线PB的斜率k2互为相反数,
k1+k2=

∵(2y1-3)(x2-1)+(2y2-3)(x1-1)
=(x1+2m-3)(x2-1)+(x2+2m-3)(x1-1)
=2x1x2+(2m-4)(x1+x2)+6-4m
=2(m2-3)+(2m-4)(-m)+6-4m=0
所以,k1+k2=0,
因此|PM|=|PN|.
分析:(1)由b>
 ,知
,知 ,所以
,所以 ,设所求椭圆方程为
,设所求椭圆方程为 ,把点P(1,
,把点P(1, )代入,能求出椭圆方程.
)代入,能求出椭圆方程.(2)
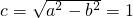 ,离心率
,离心率 ,设直线l的方程为
,设直线l的方程为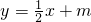 ,代入椭圆方程,得x2+mx+m2-3=0,所以x1+x2=-m,x1x2=m2-3,要证|PM|=|PN|,只需证直线PA的斜率k1与直线PB的斜率k2互为相反数.
,代入椭圆方程,得x2+mx+m2-3=0,所以x1+x2=-m,x1x2=m2-3,要证|PM|=|PN|,只需证直线PA的斜率k1与直线PB的斜率k2互为相反数.点评:通过几何量的转化考查用待定系数法求曲线方程的能力,通过直线与圆锥曲线的位置关系处理,考查学生的运算能力.通过向量与几何问题的综合,考查学生分析转化问题的能力,探究研究问题的能力,并体现了合理消元,设而不解的代数变形的思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
相关题目
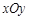 中,如图,已知椭圆E:
中,如图,已知椭圆E: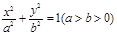 的左、右顶点分别为
的左、右顶点分别为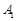 、
、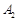 ,
,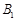 、
、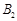 .设直线
.设直线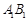 的倾斜角的正弦值为
的倾斜角的正弦值为 ,圆
,圆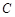 与以线段
与以线段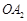 为直径的圆
为直径的圆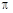 ,求圆
,求圆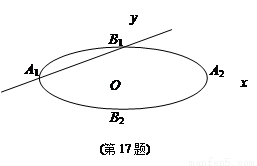

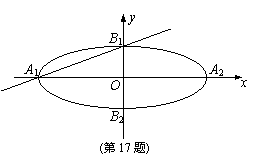 下顶点分别为
下顶点分别为 的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为
的左、右顶点分别为A1、A2,上、下顶点分别为B1、B2.设直线A1B1的倾斜角的正弦值为 ,圆C与以线段OA2为直径的圆关于直线A1B1对称.
,圆C与以线段OA2为直径的圆关于直线A1B1对称.