题目内容

利用平面向量证明：顺次连结菱形四边中点的四边形是矩形.

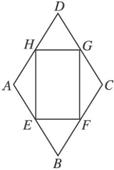
证明：如图，设E、F、G、H分别是菱形ABCD的边AB、BC、CD、DA的中点，则=+=（+）=，= +=（+）=.

∴=,∴EFHG,故有EFGH.①

∵=+=（+）=（-），

∴·=（+）（-）

=（||2-||2）=0，

∴⊥.②

由①②知，EFGH是矩形.

练习册系列答案
相关题目
请先阅读：
设平面向量
a
=（a1，a2），
b
=（b1，b2），且
a
与
b
的夹角为θ，
因为
a
•
b
=|
a
||
b
|cosθ，
所以
a
•
b
≤|
a
||
b
|．
即a1b1+a2b2≤
a
2
1
+
a
2
2
×
b
2
1
+
b
2
2
，
当且仅当θ=0时，等号成立．
（I）利用上述想法（或其他方法），结合空间向量，证明：对于任意a1，a2，a3，b1，b2，b3∈R，都有(a1b1+a2b2+a3b3)2≤(
a
2
1
+
a
2
2
+
a
2
3
)(
b
2
1
+
b
2
2
+
b
2
3
)成立；
（II）试求函数y=
x
+
2x-2
+
8-3x
的最大值．

平面向量在几何中有哪些应用?在利用平面向量解决物理问题时，应该包括哪些解题步骤?

已知A（—2,4）、B（3,—1）、C（—3,—4）且,,求点M、N的坐标及向量的坐标.

[解题思路]： 利用平面向量的基本本概念及其坐标表示求解。

已知平面向量

证明：；

若存在不同时为零的实数和，使，且，试求函数关系式。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网