题目内容
在△ABC中,射影定理可表示为a=bcosC+ccosB.?其中a、b、c依次为角A、B、C的对边,类比以上定理,给出空间四面体性质的猜想.?
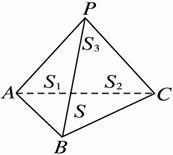
解:如图,在四面体P—ABC中,S1、S2、S3、S分别表示△PAB、△PBC、△PCA、△ABC的面积,α、β、γ依次表示面PAB、面PBC、面PCA与底面ABC所成二面角的大小.我们猜想将射影定理类比推理到三维空间,其表现形式应为S=S1cosα+S2cosβ+S3cosγ.(其正确性,同学们可自己证明)?
温馨提示:运用类比推理的方法,可以帮助我们发现问题、探索规律.不少定理、公式就是运用这种方法提出,再经过严格的证明得到的.
练习册系列答案
全能测控期末小状元系列答案
相关题目
相切。
的直线与曲线M相交于A，B两点，A，B在直线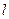
上的射影是
。求梯形
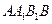的面积；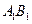
上的动点，当△ABC为直角三角形时，求点C的坐标。
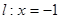相切。 
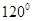的直线与曲线M相交于A，B两点，A，B在直线
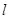上的射影是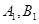
。求梯形
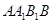的面积；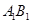
上的动点，当△ABC为直角三角形时，求点C的坐标。