题目内容
已知圆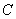 过点
过点 ,且圆心
,且圆心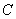 在直线
在直线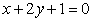 上。
上。
(I) 求圆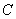 的方程;
的方程;
(II)问是否存在满足以下两个条件的直线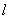 : ①斜率为
: ①斜率为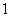 ;②直线被圆
;②直线被圆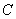 截得的弦为
截得的弦为
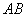 ,以
,以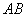 为直径的圆
为直径的圆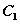 过原点.
过原点.
若存在这样的直线,请求出其方程;若不存在,说明理由.
解:(1)设圆C的方程为
则 解得D=-6,E=4,F=4
解得D=-6,E=4,F=4
所以圆C方程为
(2)设直线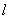 存在,其方程为
存在,其方程为 ,它与圆C的交点设为A
,它与圆C的交点设为A 、B
、B
则由 得
得 (*)
(*)
∴ 
∴ =
= 因为AB为直径,所以,
因为AB为直径,所以,

得 ,
,
∴ ,
,
即 ,
, ,∴
,∴ 或
或
容易验证 或
或 时方程(*)有实根.
时方程(*)有实根.
故存在这样的直线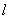 有两条,其方程是
有两条,其方程是 或
或 .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 中,角
中,角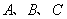 所对的边分别为
所对的边分别为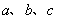 ,且满足
,且满足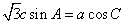
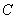 的大小;
的大小;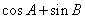 的取值范围.
的取值范围. 的离心率为
的离心率为 ,则双曲线
,则双曲线 的渐近线方程
的渐近线方程 上的一点
上的一点 的圆的切线方程是
的圆的切线方程是  B.
B. 
 D.
D. 
 所在平面,
所在平面, 的直径,
的直径, ,
, ,
, ; ②
; ② ;③
;③ ; ④平面
; ④平面 平面
平面
 是直角三角形
是直角三角形
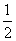 ,则周末去踢球,否则去图书馆.则小波周末去图书馆的概率是
,则周末去踢球,否则去图书馆.则小波周末去图书馆的概率是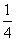 B.
B. 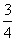 C.
C. 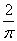
 有五个互不相等的实根,则
有五个互不相等的实根,则 的取值
的取值 B.
B. 
 D.
D. 
 中
中 为棱
为棱 的中点(如图1),用过点
的中点(如图1),用过点 的平
的平



 A. B. C. D.
A. B. C. D. 的图象为( )
的图象为( )
