题目内容
已知平面直角坐标系下的一列点Pn(an,bn)满足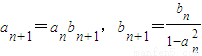 ,且
,且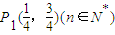 .
.(Ⅰ) 求点P2坐标,并写出过点P1,P2的直线L的方程;
(Ⅱ) 猜想点Pn(n≥2)与直线L的位置关系,并加以证明;
(Ⅲ) 若c1=1,cn+1=bncn,Sn=c1a2+c2a3+…+cnan+1,求
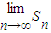 的值.
的值.
【答案】分析:(Ⅰ)由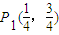 ,知
,知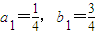 ,
,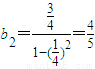 ,
, ,由此能求出过点P1,P2直线L的方程.
,由此能求出过点P1,P2直线L的方程.
(Ⅱ)由P2坐标为(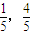 )得
)得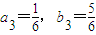 ,所以点P3∈L,猜想点Pn(n≥3,n∈N)在直线L上,再用数学归纳法证明.
,所以点P3∈L,猜想点Pn(n≥3,n∈N)在直线L上,再用数学归纳法证明.
(Ⅲ)由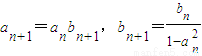 ,ak+bk=1,知an≠0,an≠±1,所以
,ak+bk=1,知an≠0,an≠±1,所以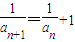 ,
, 是等差数列,由此入手能够导出
是等差数列,由此入手能够导出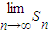 的值.
的值.
解答:解:(Ⅰ)∵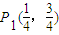 ,
,
∴ ,
,
∴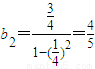 ,
,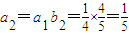 ,
,
∴P2坐标为(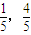 ),(2分)
),(2分)
∴过点P1,P2直线L的方程为x+y=1,(4分)
(Ⅱ)由P2坐标为(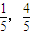 )得
)得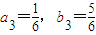 ,
,
∴点P3∈L,
猜想点Pn(n≥3,n∈N)在直线L上,以下用数学归纳法证明:
当n=3时,点P3∈L,(5分)
假设当n=k(k≥2)时,命题成立,即点Pk∈L,
∴ak+bk=1,(6分)
则当n=k+1时,ak+1+bk+1=akbk+1+bk+1
=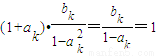 ,(7分)
,(7分)
∴点Pn∈L(n≥3),(8分)
(Ⅲ)由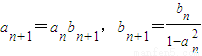 ,ak+bk=1,
,ak+bk=1,
∴an≠0,an≠±1,
∴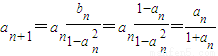 ,
,
∴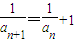 ,
,
∴ 是等差数列,
是等差数列,
∴ ,(9分)
,(9分)
∴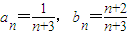 ,
,
∵cn+1=bncn,
∴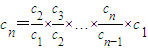 ,
,
= ,(10分)
,(10分)
∴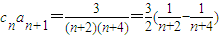 (11分)
(11分)
∴Sn=c1a2+c2a3+…+cnan+1
=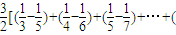
 +(
+(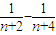 )]
)]
= ,
,
∴ =
=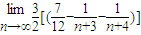
=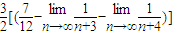 =
= .(12分)
.(12分)
点评:本题考查数列和解析几何的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.
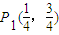 ,知
,知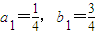 ,
,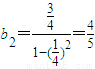 ,
, ,由此能求出过点P1,P2直线L的方程.
,由此能求出过点P1,P2直线L的方程.(Ⅱ)由P2坐标为(
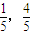 )得
)得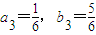 ,所以点P3∈L,猜想点Pn(n≥3,n∈N)在直线L上,再用数学归纳法证明.
,所以点P3∈L,猜想点Pn(n≥3,n∈N)在直线L上,再用数学归纳法证明.(Ⅲ)由
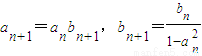 ,ak+bk=1,知an≠0,an≠±1,所以
,ak+bk=1,知an≠0,an≠±1,所以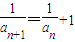 ,
, 是等差数列,由此入手能够导出
是等差数列,由此入手能够导出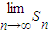 的值.
的值.解答:解:(Ⅰ)∵
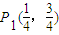 ,
,∴
 ,
,∴
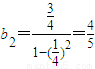 ,
,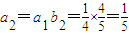 ,
,∴P2坐标为(
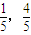 ),(2分)
),(2分)∴过点P1,P2直线L的方程为x+y=1,(4分)
(Ⅱ)由P2坐标为(
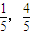 )得
)得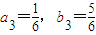 ,
,∴点P3∈L,
猜想点Pn(n≥3,n∈N)在直线L上,以下用数学归纳法证明:
当n=3时,点P3∈L,(5分)
假设当n=k(k≥2)时,命题成立,即点Pk∈L,
∴ak+bk=1,(6分)
则当n=k+1时,ak+1+bk+1=akbk+1+bk+1
=
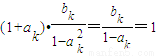 ,(7分)
,(7分)∴点Pn∈L(n≥3),(8分)
(Ⅲ)由
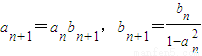 ,ak+bk=1,
,ak+bk=1,∴an≠0,an≠±1,
∴
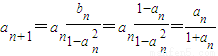 ,
,∴
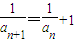 ,
,∴
 是等差数列,
是等差数列,∴
 ,(9分)
,(9分)∴
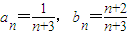 ,
,∵cn+1=bncn,
∴
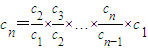 ,
,=
 ,(10分)
,(10分)∴
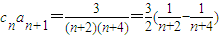 (11分)
(11分)∴Sn=c1a2+c2a3+…+cnan+1
=
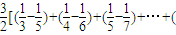
 +(
+(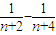 )]
)]=
 ,
,∴
 =
=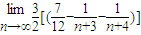
=
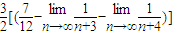 =
= .(12分)
.(12分)点评:本题考查数列和解析几何的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目