题目内容

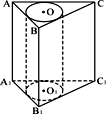
如图所示，直三棱柱ABC-A1B1C1的侧棱AA1 = 6，底面三角形的边AB = 3，BC = 4，AC =5，以上、下底的内切圆为底面，挖去一个圆柱，求剩余部分形成的几何体的体积.

    V=36-


解析:

由已知AC= AB+BC △ABC为直角三角形                 

设△ABC内切圆半径为R，则有    

  直三棱柱ABC-A1B1C1的体积V棱柱= S△ABC AA1 ==36 

内切圆为底面的圆柱体积V圆柱=             

剩余部分形成的几何体的体积    V=V棱柱-V圆柱 =36-    

练习册系列答案
相关题目
精英家教网如图所示，直三棱柱ABC-A1B1C1的各条棱长均为a，D是侧棱CC1的中点．
（1）求证：平面AB1D⊥平面ABB1A1；
（2）求异面直线AB1与BC所成角的余弦值；
（3）求平面AB1D与平面ABC所成二面角（锐角）的大小．
如图所示，直三棱柱ABC-A1B1C1中，AB⊥AC，D，E分别为AA1，B1C的中点，若记
AB
=
a
，
AC
=
b
，
AA
=
c
，则
DE
=
1
2
a
+
1
2
b
1
2
a
+
1
2
b
（用
a
，
b
，
c
表示）．
如图所示，直三棱柱ABC-A'B'C'中，∠BCA=90°，CA=CB=1，AA'=2，M，N分别是A'B'、A'A的中点．
（1）求证：A'B⊥C'M；
（2）求异面直线BA'与CB'所成交的大小；
（3）（理）求BN与平面CNB'所称的角的大小；
（4）（理）求二面角A-BN-C的大小．
如图所示，直三棱柱ABC—A1B1C1中，底面是等腰直角三角形，∠ACB=90°,AC=1,AA1=,点D是AB的中点.

（1）求证：CD⊥平面ABB1A1；

（2）求二面角A-A1B-C的平面角的正切值;

（3）求三棱锥B1—A1BC的体积；

（4）求BC1与平面A1BC所成角的正弦值.
如图所示,在直三棱柱ABC—A1B1C1中,∠ABC=90°,D为棱AC的中点,且AB=BC=BB1=a.

(1)求证:AB1∥平面BC1D;

(2)求异面直线AB1与BC1所成的角;

(3)求点A到平面BC1D的距离.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网