题目内容
在△ABC中,角A、B、C所对的边分别为a、b、c,向量 ,
, ,若
,若 ∥
∥ .
.
(1)求角A、B、C的值;
(2)若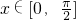 ,求函数f(x)=sinAsinx+cosBcosx的最大值与最小值、
,求函数f(x)=sinAsinx+cosBcosx的最大值与最小值、
解:(1)∵ ∥
∥ ,
,
由正弦定理,得sinAcosB=sinBcosA,∴sin(A-B)=0,
又-π<A-B<π,∴A=B
而 ,
,
∴8 +4sin2A=9,∴4(1+cosA)+4(1-cos2A)=9,
+4sin2A=9,∴4(1+cosA)+4(1-cos2A)=9,
∴4cos2A-4cosA+1=0,∴(2cosA-1)2=0
∴ ,又0<A<π,∴
,又0<A<π,∴ ,
,
∴ .
.
(2) ,
,
∵
∴x=0时, ,
,
 时,
时, .
.
分析:(1)由 ∥
∥ 的条件得acosB=bcosA,由正弦定理把边化为角,再用两角差的正正弦公式得sin(A-B)=0,在三角形内角的范围内得A=B,由向量模的值为3,得其平方为9,用坐标来表示,得关于cosA的方程,求得cosA的值,A是三角形内角,可得一个确定的角A,从而求出其它两角.
的条件得acosB=bcosA,由正弦定理把边化为角,再用两角差的正正弦公式得sin(A-B)=0,在三角形内角的范围内得A=B,由向量模的值为3,得其平方为9,用坐标来表示,得关于cosA的方程,求得cosA的值,A是三角形内角,可得一个确定的角A,从而求出其它两角.
(2)用两角和的正弦公式把f(x)化为f(x)=sin(x+ )的形式,由
)的形式,由
点评:此题是解三角形与三角函数的综合运用,在求角时,得到一个关于三角函数的等式,把这个式子要么全化成角,要么全化成边;求三角函数最值时,一般要把式子化为
y=Asin(ωx+φ)形式.
 ∥
∥ ,
,由正弦定理,得sinAcosB=sinBcosA,∴sin(A-B)=0,
又-π<A-B<π,∴A=B
而
 ,
,∴8
 +4sin2A=9,∴4(1+cosA)+4(1-cos2A)=9,
+4sin2A=9,∴4(1+cosA)+4(1-cos2A)=9,∴4cos2A-4cosA+1=0,∴(2cosA-1)2=0
∴
 ,又0<A<π,∴
,又0<A<π,∴ ,
,∴
 .
.(2)
 ,
,∵

∴x=0时,
 ,
, 时,
时, .
.分析:(1)由
 ∥
∥ 的条件得acosB=bcosA,由正弦定理把边化为角,再用两角差的正正弦公式得sin(A-B)=0,在三角形内角的范围内得A=B,由向量模的值为3,得其平方为9,用坐标来表示,得关于cosA的方程,求得cosA的值,A是三角形内角,可得一个确定的角A,从而求出其它两角.
的条件得acosB=bcosA,由正弦定理把边化为角,再用两角差的正正弦公式得sin(A-B)=0,在三角形内角的范围内得A=B,由向量模的值为3,得其平方为9,用坐标来表示,得关于cosA的方程,求得cosA的值,A是三角形内角,可得一个确定的角A,从而求出其它两角.(2)用两角和的正弦公式把f(x)化为f(x)=sin(x+
 )的形式,由
)的形式,由点评:此题是解三角形与三角函数的综合运用,在求角时,得到一个关于三角函数的等式,把这个式子要么全化成角,要么全化成边;求三角函数最值时,一般要把式子化为
y=Asin(ωx+φ)形式.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |