题目内容
椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,求此椭圆的离心率.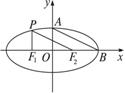
解:如图,设椭圆的方程为![]() =1(a>b>0),
=1(a>b>0),

则F1(-c,0)、F2(c,0)、A(0,b)、B(a,0).
直线PF1的方程为x=-c,代入方程![]() =1,得y=±
=1,得y=±![]() ,∴P(-c,
,∴P(-c,![]() ).
).
∵PF2∥AB,且![]() =
=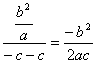 ,又kAB=
,又kAB=![]() ,∴由
,∴由![]() =kAB,得
=kAB,得![]() =
=![]() .
.
∴b=2c,a=![]() c.∴e=
c.∴e=![]() .
.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
