Question

已知等差数列{a_n}中,a₅+a₆+a₇=15,a₅·a₆·a₇=45,求数列{a_n}的通项公式.

   

Answer 1

思路分析:欲求等差数列的通项公式,只需求出首项a₁与公差d,根据条件可设出a₁与d,列方程组求解,也可以根据等差数列性质求解.

解:∵a₅+a₆+a₇=15,

∴3a₆=15,a₆=5.

∴由已知可得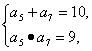

    解得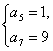或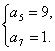

    当a₅=1,d=4时,

    通项公式为a_n=a₅+(n-5)d=1+(n-5)×4,即a_n=4n-19;

    当a₅=9,d=-4时,

    通项公式为a_n=9+(n-5)·(-4),即为a_n=-4n+29.