Question

点P是△ABC所在平面外一点，A′、B′、C′分别是△PBC、△PCA、△PAB的重心，求证：

(1)平面A′B′C′∥平面ABC；

(2)A′B′= AB.

Answer 1

【探究】 由三角形重心易联想三角形的中线交点，且交点分中线的比为2∶1，在图中取AB、BC、CA的中点M、N、Q，连结后即可证明.

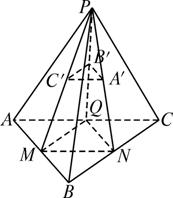
证明：(1)如图所示，取AB、BC、CA的中点M、N、Q，连结PM、PN、PQ、MN、NQ、QM，由A′、B′、C′为△PBC、△PCA、△PAB的重心，

∴A′、B′、C′分别在PN、PQ、PM上，且PC′∶PM=PA′∶PN=PB′∶PQ=2∶3.

在△PMN中，，

∴C′A′∥MN.又M、N为△ABC的边AB、BC的中点，∴MN∥AC.

∴A′C′∥AC.∴A′C′∥平面ABC.

同理，A′B′∥平面ABC.

∴平面A′B′C′∥平面ABC.

(2)由(1)知.

【规律总结】 利用重心性质可得线段成比例，从而可以得到线线平行，由线面平行的判定定理又可推得线面平行，从而最后推得面面平行，要理解并掌握三者之间的紧密联系、相互转化.