题目内容
已知等差数列{an}的公差d>0,其前n项和为Sn,若S3=12,且2a1,a2,1+a3成等比数列.
(I)求{an}的通项公式;
(II)记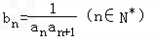 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
(I)求{an}的通项公式;
(II)记
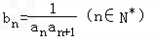 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.解:(I)由题得: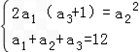
即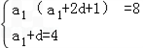 ,
,
得d2+d﹣12=0.
∵d>0,
∴d=3,a1=1.
∴{an}的通项公式an=1+3(n﹣1)=3n﹣2.
(II)∵bn=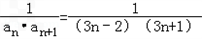 =
= (
(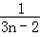 ﹣
﹣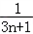 ).
).
∴Tn=b1+b2+b3+…+bn
= [(1﹣
[(1﹣ )+(
)+( ﹣
﹣ )+…+(
)+…+(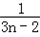 ﹣
﹣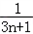 )]
)]
= (1﹣
(1﹣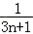 )
)
=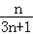 .
.
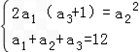
即
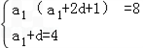 ,
,得d2+d﹣12=0.
∵d>0,
∴d=3,a1=1.
∴{an}的通项公式an=1+3(n﹣1)=3n﹣2.
(II)∵bn=
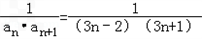 =
= (
(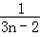 ﹣
﹣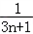 ).
).∴Tn=b1+b2+b3+…+bn
=
 [(1﹣
[(1﹣ )+(
)+( ﹣
﹣ )+…+(
)+…+(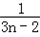 ﹣
﹣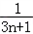 )]
)]=
 (1﹣
(1﹣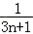 )
)=
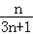 .
.
练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.