题目内容
在数列{an}中,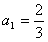 ,且对任意的n∈N*都有
,且对任意的n∈N*都有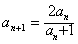 。
。
(1)求证: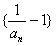 是等比数列;
是等比数列;
(2)若对任意的n∈N*都有an+1<pan,求实数p的取值范围。
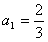 ,且对任意的n∈N*都有
,且对任意的n∈N*都有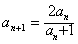 。
。(1)求证:
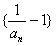 是等比数列;
是等比数列;(2)若对任意的n∈N*都有an+1<pan,求实数p的取值范围。
解:(1)证明:由 ,
,
得
又由 ,得
,得
∴ 是以
是以 为首项,以
为首项,以 为公比的等比数列。
为公比的等比数列。
(2)解:由(1),可得
即
∵
∴
显然,当n=1时, 值最大,最大值为
值最大,最大值为
∴实数p的取值范围为 。
。
 ,
,得

又由
 ,得
,得
∴
 是以
是以 为首项,以
为首项,以 为公比的等比数列。
为公比的等比数列。(2)解:由(1),可得

即

∵

∴

显然,当n=1时,
 值最大,最大值为
值最大,最大值为
∴实数p的取值范围为
 。
。
练习册系列答案
相关题目