Question

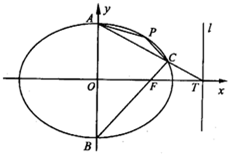（2011•江苏二模）如图，在平面直角坐标系xOy中，椭圆的中心在原点O，右焦点F在x轴上，椭圆与y轴交于A、B两点，其右准线l与x轴交于T点，直线BF交于椭圆于C点，P为椭圆上弧AC上的一点．
（1）求证：A，C，T三点共线；
（2）如果

BF

=3

FC

，四边形APCB的面积最大值为

6 +2

3

，求此时椭圆的方程和P点坐标．

Answer 1

分析：（1）设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)，求出直线AT，BF的交点，验证交点在椭圆上，从而可知A，C，T三点共线；
（2）过C作CE⊥x轴，垂足为E，△OBF∽△ECF，求得C的坐标，代入椭圆方程可得a²=2c²，b²=c²
设P（x₀，y₀），可求|AC|=

2

3

5

c，S△ABC=

1

2

•2c•

4c

3

=

4

3

c2，又可求S△APC=

1

2

d•|AC|=

1

2

•

x0+2y0-2c

5

•

2 5 c

3

=

x0+2y0-2c

3

•c，要求四边形APCB的面积最大值，只要求x₀+2y₀的最大值，从而可求椭圆方程，P的坐标．

解答：（1）证明：设椭圆方程为

x2

a2

+

y2

b2

=1(a＞b＞0)①
∴A(0，b)，B(0，-b)，T(

a2

c

，0)
∴AT：

x

a2 c

+

y

b

=1②；BF：

x

c

+

y

-b

=1③
解得交点C(

2a2c

a2+c2

，

b3

a2+c2

)，代入①得

( 2a2c a2+c2 )2

a2

+

( b3 a2+c2 )2

b2

=1
满足①式，∴C在椭圆上，A，C，T三点共线；
（2）解：过C作CE⊥x轴，垂足为E，△OBF∽△ECF
∵

BF

=3

FC

，
∴CE=

1

3

b，EF=

1

3

c
∴C(

4c

3

，

b

3

)
代入①得

( 4c 3 )2

a2

+

( b 3 )2

b2

=1
∴a²=2c²，b²=c²
设P（x₀，y₀），∴

x

2 0

+2

y

2 0

=2c2
∵C(

4c

3

，

c

3

)
∴|AC|=

2

3

5

c，S△ABC=

1

2

•2c•

4c

3

=

4

3

c2
直线AC的方程为：x+2y-2c=0
P到直线AC的距离为d=

|x0+2y0-2c|

5

=

x0+2y0-2c

5

S△APC=

1

2

d•|AC|=

1

2

•

x0+2y0-2c

5

•

2 5 c

3

=

x0+2y0-2c

3

•c
要求四边形APCB的面积最大值，只要求x₀+2y₀的最大值
∵(x0+2y0)2≤

x

2 0

+4

y

2 0

+2(

x

2 0

+

y

2 0

)=3(

x

2 0

+2

y

2 0

)=6c2
∴x0+2y0≤

6

c
当且仅当x0=y0=

6

3

c时，x₀+2y₀的最大值为

6

c
∴四边形APCB的面积最大值为

6 -2

3

c2+

4

3

c2=

6 +2

3

c2=

6 +2

3

∴c²=1，a²=2，b²=1
∴椭圆方程为

x2

2

+y2=1，P的坐标为(

6

3

，

6

3

)．

点评：本题以直线与椭圆的位置关系为载体，考查直线的交点，考查三角形面积的计算，考查三角形面积最大值的计算，综合性强．