题目内容
(2013•楚雄州模拟)(不等式选讲)已知函数f(x)=log2(|x+1|+|x-2|-m).
(1)当m=7时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
(1)当m=7时,求函数f(x)的定义域;
(2)若关于x的不等式f(x)≥2的解集是R,求m的取值范围.
分析:(1)由题设知:|x+1|+|x-2|>7,解此绝对值不等式求得函数f(x)的定义域.
(2)由题意可得,不等式即|x+1|+|x-2|≥m+4,由于x∈R时,恒有|x+1|+|x-2|≥3,故m+4≤3,由此求得m的取值范围.
(2)由题意可得,不等式即|x+1|+|x-2|≥m+4,由于x∈R时,恒有|x+1|+|x-2|≥3,故m+4≤3,由此求得m的取值范围.
解答:解:(1)由题设知:|x+1|+|x-2|>7,
不等式的解集是以下不等式组解集的并集:
,或
,或
解得函数f(x)的定义域为(-∞,-3)∪(4,+∞);
(2)不等式f(x)≥2即|x+1|+|x-2|≥m+4,
∵x∈R时,恒有|x+1|+|x-2|≥|(x+1)-(x-2)|=3,
不等式|x+1|+|x-2|≥m+4解集是R,
∴m+4≤3,m的取值范围是(-∞,-1].
不等式的解集是以下不等式组解集的并集:
|
|
|
解得函数f(x)的定义域为(-∞,-3)∪(4,+∞);
(2)不等式f(x)≥2即|x+1|+|x-2|≥m+4,
∵x∈R时,恒有|x+1|+|x-2|≥|(x+1)-(x-2)|=3,
不等式|x+1|+|x-2|≥m+4解集是R,
∴m+4≤3,m的取值范围是(-∞,-1].
点评:本题主要考查分式不等式的解法,函数的恒成立问题,体现了等价转化和分类讨论的数学思想,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
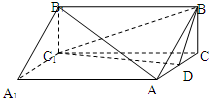 (2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.
(2013•楚雄州模拟)如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,BC⊥AC,AC=BC=2,AA1=3,D为AC的中点.