题目内容
已知数列{an}为等差数列,且公差d≠0,其中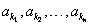 恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn.
恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn.
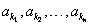 恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn.
恰为等比数列,若k1=1,k2=5,k3=17,求k1+k2+…+kn. 解:设等差数列{an}的首项为a1,公差为d,
则由题意,得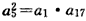 ,解得a1=2d,
,解得a1=2d,
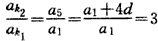 ,
,
∴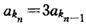 ,
,
即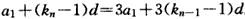 ,
,
∴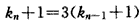 ,即
,即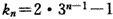 ,
,
∴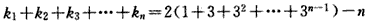
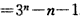 。
。
则由题意,得
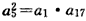 ,解得a1=2d,
,解得a1=2d,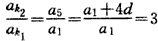 ,
,∴
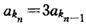 ,
,即
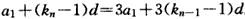 ,
,∴
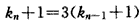 ,即
,即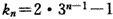 ,
,∴
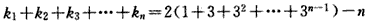
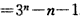 。
。 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

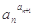 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4