题目内容
已知函数 (m>0,m≠1)的图象恒通过定点(a,b).设椭圆E的方程为
(m>0,m≠1)的图象恒通过定点(a,b).设椭圆E的方程为 (a>b>0).
(a>b>0).(1)求椭圆E的方程.
(2)若动点T(t,0)在椭圆E长轴上移动,点T关于直线
 的对称点为S(m,n),求
的对称点为S(m,n),求 的取值范围.
的取值范围.
【答案】分析:(1)先根据函数的解析式求出定点(a,b)的坐标,进而得到a和b的值,从而得到椭圆E的方程.
(2)利用点与其对称点的连线与对称轴垂直,以及点与其对称点的连线的中点在对称轴上,求出对称点S(m,n),
设ϕ(t)= ,利用它的导数符号判断其单调性,由单调性求ϕ(t)的最值,进而得到
,利用它的导数符号判断其单调性,由单调性求ϕ(t)的最值,进而得到 的取值范围.
的取值范围.
解答:解:(1)∵当x=2时, ,
,
∴函数f(x)的图象通过定点 .
.
∴
所求椭圆的方程为 .
.
(2)∵点T与点S关于直线 对称,
对称,
∴ ,
,
解方程组得 .
.
设 ,
,
∵ϕ′(t)=-2t2-1<0,
∴ϕ(t)在区间[-2,2]上是减函数.
∵ϕ(-2)=11,ϕ(2)=-9,
∴ 的取值范围是[-9,11].
的取值范围是[-9,11].
点评:本题考查椭圆的标准方程和椭圆的性质,求一个点关于直线的对称点的方法,以及利用导数判断函数的单调性,再由单调性求函数的值域的方法.
(2)利用点与其对称点的连线与对称轴垂直,以及点与其对称点的连线的中点在对称轴上,求出对称点S(m,n),
设ϕ(t)=
 ,利用它的导数符号判断其单调性,由单调性求ϕ(t)的最值,进而得到
,利用它的导数符号判断其单调性,由单调性求ϕ(t)的最值,进而得到 的取值范围.
的取值范围.解答:解:(1)∵当x=2时,
 ,
,∴函数f(x)的图象通过定点
 .
.∴

所求椭圆的方程为
 .
.(2)∵点T与点S关于直线
 对称,
对称,∴
 ,
,解方程组得
 .
.设
 ,
,∵ϕ′(t)=-2t2-1<0,
∴ϕ(t)在区间[-2,2]上是减函数.
∵ϕ(-2)=11,ϕ(2)=-9,
∴
 的取值范围是[-9,11].
的取值范围是[-9,11].点评:本题考查椭圆的标准方程和椭圆的性质,求一个点关于直线的对称点的方法,以及利用导数判断函数的单调性,再由单调性求函数的值域的方法.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知函数f(x)=ax3+bx2的图象在点(-1,2)处的切线恰好与x-3y=0垂直,又f(x)在区间[m,m+1]上单调递增,则实数m的取值范围是( )
| A、m≤-3 | B、m≥0 | C、m<-3或m>0 | D、m≤-3或m≥0 |
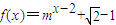 (m>0,m≠1)的图象恒通过定点(a,b).设椭圆E的方程为
(m>0,m≠1)的图象恒通过定点(a,b).设椭圆E的方程为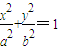 (a>b>0).
(a>b>0).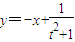 的对称点为S(m,n),求
的对称点为S(m,n),求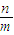 的取值范围.
的取值范围.