题目内容

在△ABC中，已知三边长分别为a=32cm，b=23cm，c=37cm，求△ABC的面积．
由a=32cm，b=23cm，c=37cm，
根据余弦定理得cosC=
a2+b2-c2
2ab
=
322+232-372
2×32×23
=
1
8
，（4分）
又C∈（0，π），∴sinC=
1-cos2C
=
3
7
8
，（8分）
所以S△ABC=
1
2
absinC=
1
2
×32×23×
3
7
8
=138
7
cm2．（12分）
练习册系列答案
相关题目
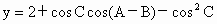在△ABC中，已知三内角∠A、∠B、∠C成等差数列，其对边分别为a、b、c，且c-a等于边AC上的高h．则sin
C-A
2
=
1
2
1
2
．
在△ABC中，已知三个内角A、B、C的对边分别是a、b、c，向量
m
=（a，b），
n
=（cos（2π-B），sin（
π
2
+A）），若a≠b且
m
∥
n
，
（Ⅰ）试求内角C的大小；
（Ⅱ）若a=6，b=8，△ABC的外接圆圆心为O，点P位于劣弧
AC
上，∠PAB=60°，求四边形ABCP的面积．

在△ABC中，已知三个顶点A(2，4)，B(－1，2)，C(1，0)，点P(x，y)在△ABC内部及边界运动，则z＝x－y的最大值为

[　　]
A．

1

B．

－3

C．

－1

D．

3

在△ABC中，已知三内角A、B、C满足关系式．

(1)求证：任意变换A、B、C的位置y的值不变．

(2)求y最大值．

在△ABC中，已知三内角A、B、C顺次成等差数列，则 的值是________

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网