题目内容
求以圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0的公共弦为直径的圆的方程.
分析:先确定公共弦的方程,再求出公共弦为直径的圆的圆心坐标、半径,即可得到公共弦为直径的圆的圆的方程.
解答:解:∵圆C1:x2+y2-12x-2y-13=0和圆C2:x2+y2+12x+16y-25=0,
∴两圆相减可得公共弦方程为l:4x+3y-2=0
又∵圆C1:x2+y2-12x-2y-13=0的圆心坐标为(6,1),半径为5
;
圆C2:x2+y2+12x+16y-25=0的圆心坐标为(-6,-8),半径为5
,
∴C1C2的方程为3x-4y-14=0
∴联立
可得公共弦为直径的圆的圆心坐标为(2,-2),
∵(6,1)到公共弦的距离为5
∴公共弦为直径的圆的半径为5
∴公共弦为直径的圆的方程为(x-2)2+(y+2)2=25.
∴两圆相减可得公共弦方程为l:4x+3y-2=0
又∵圆C1:x2+y2-12x-2y-13=0的圆心坐标为(6,1),半径为5
| 2 |
圆C2:x2+y2+12x+16y-25=0的圆心坐标为(-6,-8),半径为5
| 5 |
∴C1C2的方程为3x-4y-14=0
∴联立
|
∵(6,1)到公共弦的距离为5
∴公共弦为直径的圆的半径为5
∴公共弦为直径的圆的方程为(x-2)2+(y+2)2=25.
点评:本题考查圆与圆的位置关系,考查圆的方程的确定,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
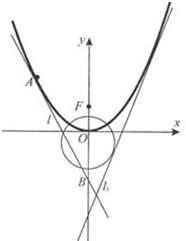 如图,已知直线
如图,已知直线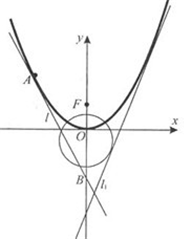 如图,已知直线
如图,已知直线 x-y+3+8
x-y+3+8 和圆C1:x2+y2+8x+F=0.若直线l被圆C1截得的弦长为2
和圆C1:x2+y2+8x+F=0.若直线l被圆C1截得的弦长为2 .
. x-y+3+8
x-y+3+8 和圆C1:x2+y2+8x+F=0.若直线l被圆C1截得的弦长为2
和圆C1:x2+y2+8x+F=0.若直线l被圆C1截得的弦长为2 .
.