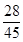题目内容
在10件产品中有2件次品,连续抽3次,每次抽1件,求:(1)不放回抽样时,抽到次品数ξ的分布列;
(2)放回抽样时,抽到次品数η的分布列.
解析:(1)P(ξ=0)=![]() ,P(ξ=1)=
,P(ξ=1)= ![]() ,
,
P(ξ=2)=![]() ,
,
所以ξ的分布列为
ξ | 0 | 1 | 2 |
P |
|
|
|
(2)P(η=k)= ![]() ·0.8 3-k·0.2k(k=0,1,2,3),所以η的分布列为
·0.8 3-k·0.2k(k=0,1,2,3),所以η的分布列为
η | 0 | 1 | 2 | 3 |
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知在10件产品中有2件次品,现从中任意抽取2件产品,则至少抽出1件次品的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
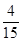 B.
B.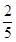 C.
C.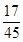 D.
D.