Question

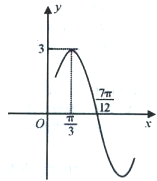已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，|φ|＜

π

2

）的部分图象如图所示．
（1）求f（x）的解析式；
（2）把函数y=f（x）的图象向左平移

π

3

个单位，得到函数y=g（x）的图象．请写出g（x）的表达式，并求出函数y=g（x）的对称轴和对称中心．

Answer 1

分析：（1）由图象的顶点坐标求出A，由周期求出ω，再由五点法作图求得∅的值，从而得到f（x）的解析式．
（2）根据函数y=Asin（ωx+∅）的图象变换规律求出g（x）的解析式，从而求出它的对称轴和对称中心．

解答：解：（1）由函数的图象可得A=3，

1

4

×

2π

ω

=

7π

12

-

π

3

，解得ω=2．
再由五点法作图可得 2×

π

3

+∅=

π

2

，故∅=-

π

6

，故f（x）的解析式为 f（x）=3sin（2x-

π

6

）．
（2）把函数y=f（x）的图象向左平移

π

3

个单位，得到函数y=3sin[2（x+

π

3

）-

π

6

]=3sin（2x+

π

2

）=3cos2x的图象．
故y=g（x）=3cos2x．
令2x=kπ，可得 x=

kπ

2

，k∈z，故g（x）的对称轴为  x=

kπ

2

，k∈z．
令2x=kπ+

π

2

，可得 x=

kπ

2

+

π

4

，k∈z，故g（x）的对称中心为（

kπ

2

+

π

4

，0）．

点评：本题主要考查由函数y=Asin（ωx+∅）的部分图象求函数的解析式，余弦函数的对称性，函数y=Asin（ωx+∅）的图象变换规律，属于中档题．