题目内容
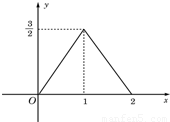
 如图所示,图象为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图所示,图象为函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求f(x)的解析式.
(2)已知g(α)=
| 3 |
| π |
| 4 |
| 3 |
分析:(1)通过函数的图象求出A,横坐标的差值求出函数的周期,得到ω,利用函数经过的特殊点求解φ,得到函数的解析式.
(2)通过g(α)=
f(α-
)+f(α),利用两角和与差的三角函数函数函数为α的三角函数,tanα=
,通过“1”的代换,求出g(x)的值.
(2)通过g(α)=
| 3 |
| π |
| 4 |
| 3 |
解答:解:(1)由图象知,A=1,
=
-(-
)=
,
∴T=π
∴ω=
=2,
又函数的图象经过(-
,0),
∴0=sin[2×(-
)+φ],
∵|φ|<
.
∴2•(-
)+φ=0,解得φ=
∴f(x)=sin(2x+
)…(6分)
(2)∵f(α)=sin(2α+
)
∴g(α)=
sin[2(α-
)+
]+sin(2α+
)
=
sin(2α-
)+sin(2α+
)
=
(sin2αcos
-cos2αsin
)+sin2αcos
+cos2αsin
=2sin2α…(10分).
∵tanα=
∴sin2α=2sinαcosα=
=
=
=
,
∴g(α)=2sin2α=
…(12分)
| T |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴T=π
∴ω=
| 2π |
| T |
又函数的图象经过(-
| π |
| 6 |
∴0=sin[2×(-
| π |
| 6 |
∵|φ|<
| π |
| 2 |
∴2•(-
| π |
| 6 |
| π |
| 3 |
∴f(x)=sin(2x+
| π |
| 3 |
(2)∵f(α)=sin(2α+
| π |
| 3 |
∴g(α)=
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
=
| 3 |
| π |
| 6 |
| π |
| 3 |
=
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
∵tanα=
| 3 |
∴sin2α=2sinαcosα=
| 2sinαcosα |
| sin2α+cos2α |
| 2tanα |
| tan2α+1 |
2
| ||
| 4 |
| ||
| 2 |
∴g(α)=2sin2α=
| 3 |
点评:本题考查三角函数的解析式的求法,同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
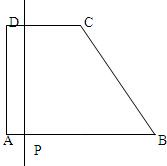
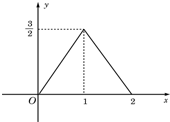 如图所示的图象所表示的函数解析式为
如图所示的图象所表示的函数解析式为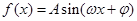
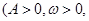
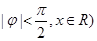 的部分图象
的部分图象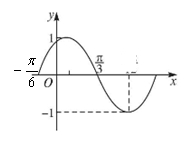
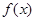 的解析式
的解析式
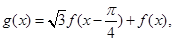 且
且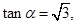 求
求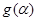 的值
的值