Question

（2006•松江区模拟）已知函数f(x)=

cos2x

1-|sinx|

，x∈(-

π

2

，

π

2

)．
（1）在坐标系中作出函数的草图；
（2）研究其值域、奇偶性和单调性，并分别加以证明．

Answer 1

分析：（1）利用零点分段法，我们可将函数函数f(x)=

cos2x

1-|sinx|

，x∈(-

π

2

，

π

2

)的解析式表示为分段函数的形式，结合正弦型函数的图象和性质及函数图象的平移变换法则，根据分段函数图象分段画的原则，即可画出函数函数f(x)=

cos2x

1-|sinx|

，x∈(-

π

2

，

π

2

)的图象．
（2）根据（1）中函数图象，我们根据图象法求函数值域，图象法判断函数奇偶性和单调性的方法，得到函数的值域、奇偶性和单调性，并可以根据奇偶性的定义和作差法进行证明．

解答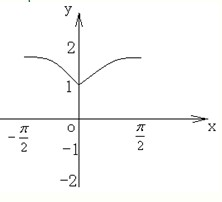：解：（1）f(x)=

cos2x

1-|sinx|

=

1+sinx，x∈[0 π 2 ) 1-sinx，x∈(- π 2 ，0)

，
（2）f（x）的值域为[1，2）．
∵f(-x)=

cos2(-x)

1-|sin(-x)|

=

cos2x

1-|sinx|

=f(x)，
∴f（x）是偶函数．
任取0≤x1＜x2＜

π

2

，
则1+sinx₁＜1+sinx₂，
即f（x₁）＜f（x₂），
∴f（x）在[0，

π

2

)上是增函数，
又f（x）是偶函数，
在对称区间函数的单调性相反
∴f（x）在(-

π

2

，0)上是减函数．

点评：本题考查的知识点是函数的图象，函数的值域，函数的单调性及其证明，函数的奇偶性及其证明，三角函数的化简求值，是函数问题比较综合的考查，其中根据零点分段法将函数的解析式化为分段函数的形式，并结合正弦型函数的图象和性质，画出函数的草图是解答本题的关键．