题目内容
在120°的二面角内放一个半球为5的球,切两个半平面于A、B两点,则这两个切点在球面上的球面距离是_________________.
![]()
解析:本题考查考生空间想象能力以及分析解决问题的能力.解题关键是将主要条件抽象出来,合理转化.

如图:设球心为O,A、B是球与平面的两个切点,平面OAB交二面角的棱于点C,由于OA、OB分别垂直于两平面,易由垂面法知∠ACB即为二面角的平面角,且由OA⊥AC,OB⊥BC,即O、A、B、C四点共圆,故∠AOB+∠ACB=180 ,故∠AOB=60 ,A、B之间的球面距离d=![]() .
.

练习册系列答案
相关题目
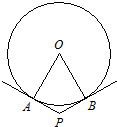 (2008•普陀区一模)在120°的二面角内放一个半径为6的球,使球与两个半平面各只有一个公共点(其过球心且垂直于二面角的棱的直截面如图所示),则这两个公共点AB之间的球面距离为
(2008•普陀区一模)在120°的二面角内放一个半径为6的球,使球与两个半平面各只有一个公共点(其过球心且垂直于二面角的棱的直截面如图所示),则这两个公共点AB之间的球面距离为