题目内容
(本小题满分12分) 如图，已知椭圆
的上顶点为
，右焦点为
，直线
与圆
相切．
（Ⅰ）求椭圆
的方程；
（Ⅱ）若不过点的动直线
与椭圆相交于
、
两点，
且
求证：直线过定点，并求出该定点
的坐标．
解: （Ⅰ）将圆
的一般方程
化为标准方程 
，
圆的圆心为
,半径
. --------------------1分
由
,
得直线
,即
,------------2分
由直线
与圆相切,得
, 
或
(舍去). ----------3分
当时, 
, 故椭圆
的方程为
-------------------4分
（Ⅱ）(解法一)由
知
,从而直线
与坐标轴不垂直, -------5分
由可设直线的方程为
，直线
的方程为
. --6分
将代入椭圆的方程
并整理得: 
,
解得
或
,因此
的坐标为
,
即
将上式中的
换成
,得
.
直线
的方程为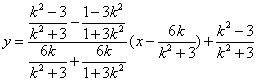
------------------10分
化简得直线的方程为
，------------------11分
因此直线过定点
.------------------12分
(解法二)
若直线存在斜率，则可设直线的方程为：
，代入椭圆的方程并整理得: 
, -------5分
由与椭圆相交于
、
两点，则
是上述关于
的方程两个不相等的实数解，从而
------6分
由得
，
整理得：
由
知
.
此时
, 因此直线过定点. 10分
若直线不存在斜率，则可设直线的方程为：
，
将代入椭圆的方程并整理得: 
,
当
时, 
,直线与椭圆不相交于两点，这与直线与椭圆相交于、两点产生矛盾!
当
时, 直线与椭圆相交于
、
两点，
是关于
的方程的两个不相等实数解，从而
但
,这与
产生矛盾!
因此直线过定点.-------12分
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
