题目内容
已知奇函数f(x)在(-∞,0)∪(0,+∞)上有意义,且在(0,+∞)上是增函数,f(1)=0,又有函数g(θ)=sin2θ+mcosθ-2m,θ∈[0,
],若集合M={m|g(θ)<0},集合N={m|f[g(θ)]<0}.
(1)求f(x)<0的解集;
(2)求M∩N.
| π | 2 |
(1)求f(x)<0的解集;
(2)求M∩N.
分析:(1)由f(x)为奇函数,在(-∞,0)上是增函数,可判断f(x)在(-∞,0)上单调性,由f(1)=0可得f(-1)=0,据此可解不等式;
(2)由(1)可去掉符号集合N中的符号“f”,从而可化简M∩N,分离出m后转化求函数的最值,用基本不等式可求得最值;
(2)由(1)可去掉符号集合N中的符号“f”,从而可化简M∩N,分离出m后转化求函数的最值,用基本不等式可求得最值;
解答:解:(1)f(x)为奇函数,f(1)=0⇒f(-1)=-f(1)=0,
f(x)在(-∞,0)上是增函数⇒f(x)在(-∞,0)上也是增函数,
⇒f(x)<0的解集为{x|x<-1或0<x<1};
(2)N={m|f[g(θ)]<0}={m|g(θ)<-1或0<g(θ)<1},
M={m|g(θ)<0}⇒M∩N={m|g(θ)<-1},
,
由θ∈[0,
]⇒cosθ-2∈[-2,-1]⇒
≤4-2
(当cosθ=2-
时,等号成立)⇒m>4-2
⇒M∩N={m|m>4-2
}.
f(x)在(-∞,0)上是增函数⇒f(x)在(-∞,0)上也是增函数,
⇒f(x)<0的解集为{x|x<-1或0<x<1};
(2)N={m|f[g(θ)]<0}={m|g(θ)<-1或0<g(θ)<1},
M={m|g(θ)<0}⇒M∩N={m|g(θ)<-1},
|
由θ∈[0,
| π |
| 2 |
| 2-cos2θ |
| 2-cosθ |
| 2 |
(当cosθ=2-
| 2 |
| 2 |
| 2 |
点评:本题考查函数的奇偶性、单调性的综合应用,考查学生运用知识解决问题的能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知奇函数f(x)在[-1,0]上单调递减,又α,β为锐角三角形的两内角,则有( )
| A、f(sinα-sinβ)≥f(cosα-cosβ) | B、f(sinα-cosβ)>f(cosα-sinβ) | C、f(sinα-cosβ)≥f(cosα-sinβ) | D、f(sinα-cosβ)<f(cosα-sinβ) |
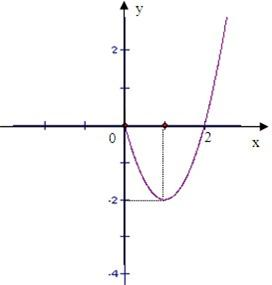 已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,
已知奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分,