题目内容
【题目】如图,已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,过点
,过点![]() 、
、![]() 分别作两条平行直线
分别作两条平行直线![]() 、
、![]() 交椭圆
交椭圆![]() 于点
于点![]() 、
、![]() 、
、![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)求四边形![]() 面积的最大值.
面积的最大值.
【答案】(1)证明见解析;(2)![]() 的最大值为6.
的最大值为6.
【解析】
试题分析:(1)圆锥曲线中证明两线段相等,一般要用解析法,计算这两条线段的长度得相等结论,直线![]() 斜率不可能为0,因此可设设
斜率不可能为0,因此可设设![]() ,
,![]() ,
,![]() :
:![]() .所
.所![]() 代入椭圆方程得出
代入椭圆方程得出![]() 的一元二次方程,从而得
的一元二次方程,从而得![]() ,由圆锥曲线上的弦长公式得
,由圆锥曲线上的弦长公式得![]() ,同理
,同理![]() 方程为
方程为![]() ,并设
,并设![]() ,
,![]() ,最后计算出
,最后计算出![]() ,它们相等;(2)原点
,它们相等;(2)原点![]() 实质上是平行四边形
实质上是平行四边形![]() 对角线的交点,而
对角线的交点,而![]() ,从而可得
,从而可得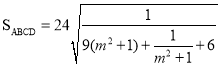 ,设
,设![]() ,因此只要求得
,因此只要求得![]() 的最小值,即可得结论,此最小值可用函数的单调性得出(可先用基本不等式求解,发现基本不等式中等号不能取到).
的最小值,即可得结论,此最小值可用函数的单调性得出(可先用基本不等式求解,发现基本不等式中等号不能取到).
试题解析:(1)设![]() ,
,![]() ,
,![]() :
:![]() .
.
联立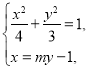 得
得![]() .
.
∴![]() ,
,![]() .
.
设![]() ,
,![]() ,由
,由![]() ,得
,得![]() :
:![]() .
.
联立 得
得![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
而![]() ,
,![]() ,
,
∴![]() .
.
(2)由(1)知四边形![]() 为平行四边形,
为平行四边形,![]() ,且
,且![]() .
.
∴![]()
![]()
![]()
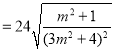
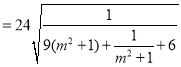 .
.
设![]() (
(![]() ),
),![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() .
.
故![]() 的最大值为6,此时
的最大值为6,此时![]() .
.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目