题目内容
已知函数
f(x)的导函数是
。对任意两个不相等的正数
，证明：
（Ⅰ）当
时，
；
（Ⅱ）当
时，
。
证明：（Ⅰ）由
得
而
①
又
∴
②
∵
∴
∵
∴
③
由①、②、③得
即
（Ⅱ）证法一：由
，得
∴
下面证明对任意两个不相等的正数
,有
恒成立
即证
成立
∵
设
，则
令
得
，列表如下：
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
∴
∴对任意两个不相等的正数
，恒有
证法二：由，得
∴
∵是两个不相等的正数
∴
设
则
，列表：
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
∴
即 
∴即对任意两个不相等的正数，恒有
练习册系列答案
名校课堂系列答案
相关题目
的图象如图所示，那么函数f (x)的图象最有可能的是( )
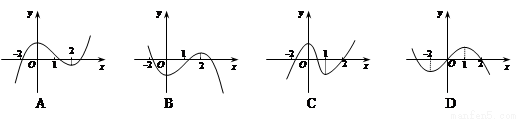
，且满足f(x)＝2x
＋ln x，则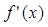
的图像如左图所示，那么函数f(x)的图像最有可能的