题目内容
(1)设函数![]() ,且数列
,且数列![]() 满足
满足![]() = 1,
= 1,![]() (n∈N,
(n∈N,![]() );求数列
);求数列![]() 的通项公式.
的通项公式.
(2)设等差数列![]() 、
、![]() 的前n项和分别为
的前n项和分别为![]() 和
和![]() ,且
,且![]()
![]() ,
,![]() ,
, ![]() ;求常数A的值及
;求常数A的值及![]() 的通项公式.
的通项公式.
(3)若![]() ,其中
,其中![]() 、
、![]() 即为(1)、(2)中的数列
即为(1)、(2)中的数列![]() 、
、![]() 的第
的第![]() 项,试求
项,试求![]()
(1)![]() .(2)
.(2)![]() ;
;![]() .
.
(3)![]()
![]()
解析:
(1) 由题意:![]() ,变形得:
,变形得:![]() ,
,
∴数列![]() 是以
是以![]() 为公比,
为公比,![]() 为首项的等比数列.
为首项的等比数列.
∴![]() ,即
,即![]() .
.
(2)∵由等差数列![]() 、
、![]() 知:
知:![]() ;
;
∴由![]() 得:
得:![]() ,
,
∴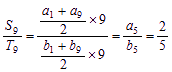 ,∵
,∵![]() ,∴
,∴![]() ,解得
,解得![]() ;
;
∴![]() ,
,![]() 和
和![]() 分别是等差数列
分别是等差数列![]() 、
、![]() 的前n项和;
的前n项和;
∴可设![]() ; ∵
; ∵![]() , ∴
, ∴![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,
,
当n≥2时,![]() .
.
综上得:![]() .
.
(3)当![]() (
(![]() N*)时,
N*)时,
![]()
![]()
当![]() (
(![]() N*)时,
N*)时,
![]()
![]()

练习册系列答案
相关题目
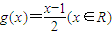 ,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.
,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.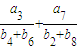 =
=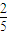 ,
,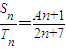 ,S2=6;求常数A的值及{an}的通项公式.
,S2=6;求常数A的值及{an}的通项公式.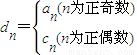 ,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.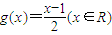 ,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.
,且数列{cn}满足c1=1,cn=g(cn-1)(n∈N,n>1);求数列{cn}的通项公式.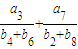 =
=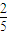 ,
,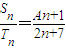 ,S2=6;求常数A的值及{an}的通项公式.
,S2=6;求常数A的值及{an}的通项公式.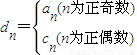 ,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.
,其中an、cn即为(1)、(2)中的数列{an}、{cn}的第n项,试求d1+d2+…+dn.