题目内容
如图所示，在正方体ABCD—A′B′C′D′中，直线AC与直线BC′所成的角为( )
A.30° B.60° C.90° D.45°
思路解析：要确定直线AC与直线BC′所成的角，容易想到利用异面直线所成的角的定义，平移其中的一条（或两条）直线，将相应的角转化为相交两直线所成的角的问题.
连结A′C′、A′B.容易得知，A′C′=AC，A′C′∥AC，∠A′C′B（或其补角）是直线AC与直线BC′所成的角.在正方体ABCD—A′B′C′D′中,A′C′=BC′=A′B，所以∠A′C′B=60°.故选B．
答案：B
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
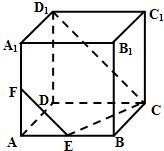如图所示，在正方体ABCD-A1B1C1D1中，E为AB的中点
（2011•宝山区二模）如图所示，在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等，则动点P所在曲线形状为（ ）
如图所示，在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等，则动点P所在曲线的形状为（ ）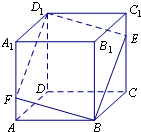
如图所示，在正方体ABCD-A1B1C1D1中，点E是棱CC1上的一个动点，平面BED1交棱AA1于点F．则下列命题中假命题是（ ）