题目内容
已知函数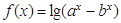 (
(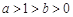 )
)
(1)求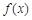 的定义域;
的定义域;
(2)问是否存在实数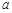 、
、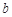 ,当
,当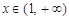 时,
时,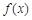 的值域为
的值域为 ,且
,且 若存在,求出
若存在,求出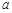 、
、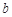 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(1)(0,+ );(2)
);(2)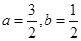
解析试题分析:(1)由题意可得对数的真数大于零即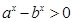 .又因为
.又因为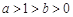 .所以可得
.所以可得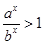 .所以可得定义域的结论.
.所以可得定义域的结论.
(2)由(1)可得在(1,+∞)上递增.又由于f(x)的值域为(0,+∞)所以f(1)=0.所以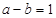 .又因为
.又因为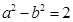 .由此可解得
.由此可解得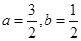 .本题通过对数的定义域,渗透参数的不等式的解法是难点.通过定义域与值域的关系建立两个等式即可求出相应的结论.
.本题通过对数的定义域,渗透参数的不等式的解法是难点.通过定义域与值域的关系建立两个等式即可求出相应的结论.
试题解析:(1)由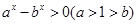 得
得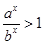 .所以x>0.所以f(x)的定义域为(0,+
.所以x>0.所以f(x)的定义域为(0,+ ).
).
(2)令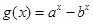 .又
.又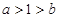 .所以g(x)在(0,+
.所以g(x)在(0,+ )上为增函数.当
)上为增函数.当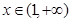 时.g(x)>1.所以g(1)=1,即
时.g(x)>1.所以g(1)=1,即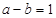 …①.又因为f(2)=lg2.所以
…①.又因为f(2)=lg2.所以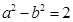 …②.解由①②得.
…②.解由①②得. 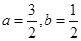 .
.
考点:1.对数的定义域.2.函数的单调性.3.含参的不等式的解法.

练习册系列答案
相关题目
 上的函数
上的函数 同时满足以下条件:
同时满足以下条件: 在(0,1)上是减函数,在(1,+∞)上是增函数;
在(0,1)上是减函数,在(1,+∞)上是增函数; 是偶函数;
是偶函数; y=x+2垂直.
y=x+2垂直. =
= ,若存在实数x∈[1,e],使
,若存在实数x∈[1,e],使 <
< 满足:对任意
满足:对任意 ,都有
,都有 成立,且
成立,且 时,
时, .
. 的值,并证明:当
的值,并证明:当 时,
时, ;
; 在
在 上递减,求实数
上递减,求实数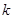 的取值范围.
的取值范围. ,x∈[1,3],
,x∈[1,3], 于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.
于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围. 满足
满足 ,当
,当 时,
时,
 ,当
,当 时,
时, 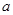 的值;
的值;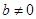 ,函数
,函数 ,
, .若对任意的
.若对任意的 ,总存在
,总存在 ,使
,使 ,求实数
,求实数 的取值范围.
的取值范围. .
.
 的图像;
的图像;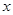 的方程
的方程 在区间
在区间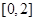 上解的个数.
上解的个数. 上的函数
上的函数 ,如果对任意
,如果对任意 ,恒有
,恒有 (
( ,
,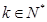 )成立,则称
)成立,则称 阶缩放函数.
阶缩放函数. 时,
时, ,求
,求 的值;
的值; ,求证:函数
,求证:函数 在
在 上无零点;
上无零点; 时,
时, ,求
,求 (
( )上的取值范围.
)上的取值范围. 上的函数
上的函数 当
当 时,
时, ,且对任意的
,且对任意的 有
有 。
。 ,
, ,恒有
,恒有 ;
; ,求
,求 的取值范围。
的取值范围。 (
( 为实常数).
为实常数). 时,证明:
时,证明: 不是奇函数;②
不是奇函数;② 是
是 上的单调递减函数.
上的单调递减函数. 与
与 的值.
的值.