题目内容
一个不透明的口袋中装有形状相同的红球、黄球和蓝球,若摸出一球为红球的概率为 ,黄球的概率为
,黄球的概率为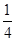 ,袋中红球有4个,则袋中蓝球的个数为( ).
,袋中红球有4个,则袋中蓝球的个数为( ).
| A.5个 | B.11个 | C.4个 | D.9个 |
B
解析试题分析:根据题意,设篮球个数为n,黄球为m个,那么根据题意,摸出一球为红球的概率为 ,黄球的概率为
,黄球的概率为 ,则说明m+n=16,同时可知m=5,n=11,故答案为B.
,则说明m+n=16,同时可知m=5,n=11,故答案为B.
考点:古典概型
点评:主要是考查了古典概型概率的运用,属于基础题。

练习册系列答案
相关题目
样本中共有5个个体,其值分别为 .若该样本的平均值为1,则样本方差为
.若该样本的平均值为1,则样本方差为
A. | B. | C. | D. |
一个三位数字的密码键,每位上的数字都在0到9这十个数字中任选,某人忘记后一个号码,那么此人开锁时,在对好前两位数码后,随意拨动最后一个数字恰好能开锁的概率为( )
| A.1/1000 | B.1/100 | C.1/10 | D.1/9 |
在某一试验中事件A出现的概率为 ,则在
,则在 次试验中
次试验中 出现
出现 次的概率为( )
次的概率为( )
A.1- | B. |
C.1- | D. |
设随机变量 的分布列为
的分布列为 ,则
,则 ()
()
A. | B. | C. | D. |
设 为两个事件,且
为两个事件,且 ,
, ,则( )
,则( )
A. 与 与 互斥 互斥 | B. 与 与 对立 对立 | C. | D.A、B、C都不对 |
随机变量 服从二项分布
服从二项分布 ~
~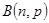 ,且
,且 则
则 等于( )
等于( )
A. | B.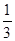 | C.1 | D.0 |
 表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于
表示平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于 的概率是( )
的概率是( )



 B.
B. C.
C.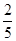 D.
D.